按如下的方法構造一個多位數:先任意寫一個整數n(0<n<10)作為第一位上的數字,將這個整數n乘以3,若積為一位數,則將其作為第2位上的數字,若積為兩位數,則將其個位數字作為第2位上的數字;再將第2位上的數字乘以3,若積為一位數,則將其作為第3位上的數字,若積為兩位數,則將其個位數字作為第3位上的數字;…以此類推.若先任意寫的一個整數n是7作為第一位上的數字,進行2020次如上操作后得到了第2021位上的數字,則第2022位上的數字是( )
【考點】規律型:數字的變化類.
【答案】A
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/24 8:0:9組卷:38引用:1難度:0.5
相似題
-
1.提出問題:把1到2022這2022個數,按順時針方向依次排列在一個圓周上,從1開始按順時針方向,保留1,擦去2,保留3,擦去4……(每隔一數;擦去一數),轉圈擦下去,最后剩下的是哪個數?
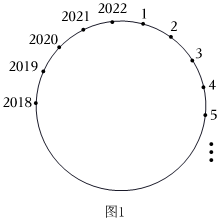
問題探究:我們先從簡單情形入手,再逐次遞進,最后猜想得出結論.
探究一:
如果只有1,2,很明顯,留下1,擦去2,最后剩下1;
如果只有1,2,3,4,如圖2所示,第一圈留下1,3擦去2,4;第二圈留下1,擦去3,最后剩下1;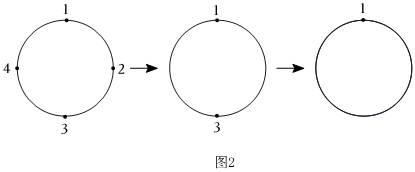
如果只有1,2,3,4,5,6,7,8,如圖3所示,第一圈留下1,3,5,7擦去2,4,6,8;第二圈留下1,5擦去3,7;第三圈留下1,擦去5;最后剩下1;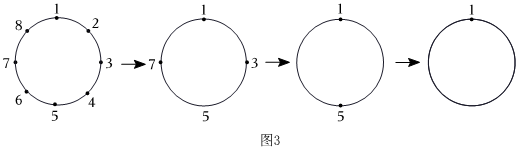
如果只有1,2,3,…,16這16個數,按順時針方向依次排列在一個圓周上,從1開始按順時針方向,保留1,擦去2,保留3,擦去4…(每隔一數,擦去一數),轉圈擦下去,最后剩下的數是 ;
探究二:
如果只有1,2,3,4,5,6,7這7個數,由探究一可知只有4個數時,最后剩下的是1,即4個數中的“第一個數”,因此只要剩下4個數,即可知最后剩下的是哪個數.也就是先擦掉7-4=3個數,擦掉的第3個數是6,它的下一個數是7,也就是剩下的4個數中的第一個是7,所以最后剩下的數就是7;
如果只有1,2,3,…,12這12個數,由探究一可知只有8個數時,最后剩下的是1,即8個數中的“第一個數”,因此只要剩下8個數,即可知最后剩下的是哪個數.也就是先擦掉12-8=4個數,擦掉的第4個數是8,它的下一個數是9,也就是剩下的8個數中的第一個是9,所以最數學試題第7頁共8頁后剩下的數就是9;
仿照上面的探究方法,回答下列問題:
如果只有1,2,3,…,26這26個數,按順時針方向依次排列在一個圓周上,從1開始按順時針方向,保留1,擦去2,保留3,擦去4……(每隔一數,擦去一數),轉圈擦下去,最后剩下的數是 ;
問題解決:
把1到2022這2022個數,按順時針方向依次排列在一個圓周上,從1開始按順時針方向,保留1,擦去2,保留3,擦去4……(每隔一數,擦去一數),轉圈擦下去,最后剩下的數是 ;
一般規律:
把1,2,3,…,n這個數,按順時針方向依次排列在一個圓周上,從1開始按順時針方向,保留1,擦去2,保留3,擦去4……(每隔一數,擦去一數),轉圈擦下去,如果2k<n<2k+1,且n和k都是正整數,則最后剩下的數是 ;(用n、k的代數式表示)
拓展延伸:
如果只有1,2,3,…,n這n個數,且n5000,n是正整數,按順時針方向依次排列在一個圓周上,從1開始按順時針方向,保留1,擦去2,保留3,擦去4…(每隔一數,擦去一數),轉圈擦下去,如果最后剩下的數是2023,則n可以為 .發布:2025/5/24 0:30:1組卷:317引用:2難度:0.2 -
2.將正偶數按照如下規律進行分組排列,依次為(2),(4,6),(8,10,12),(14,16,18,20),…,我們稱4是第2組第1個數字,16是第4組第2個數字,若2020是第m組第n個數字,則m+n=.
發布:2025/5/24 1:0:1組卷:953引用:7難度:0.6 -
3.觀察下列等式:
第1個等式:;31×2×22=11×2-12×22
第2個等式:;42×3×23=12×22-13×23
第3個等式:;53×4×24=13×23-14×24
第4個等式:;64×5×25=14×24-15×25
第5個等式:;75×6×26=15×25-16×26
……
按上述規律,回答以下問題:
(1)寫出第6個等式:;
(2)寫出你猜想的第n個等式:(用含n的等式表示),并證明.發布:2025/5/24 1:0:1組卷:212引用:3難度:0.5


