三角形是生活中常見的圖形，在一些設計中經常見到，雖其本身不是夸張的幾何圖形，但是多樣多變的三角形值得我們進行的研究．比如在勾股定理這一章中，我們知道了如何通過邊去判定一個三角形為直角三角形．類似地，我們定義：如果一個三角形兩邊的平方和等于第三邊平方的2倍，那么這個三角形就叫美妙三角形．
（1）根據美妙三角形的定義，可以判斷下列三角形一定是美妙三角形的是 DD．
A．直角三角形
B．等腰三角形
C．等腰直角三角形
D．等邊三角形
（2）在△ABC中AC=3，BC=2，AB=1，試判斷△ABC是否為美妙直角三角形，并說明理由；
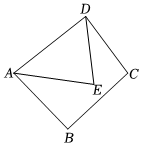
（3）如圖，在四邊形ABCD中，AB=BC，∠ABC=∠ADC=90°，E是四邊形ABCD內一點，且AE=AB，DE=DC，求證：△AED是美妙三角形．
AC
=
3
BC
=
2
【考點】三角形綜合題．
【答案】D
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/9 5:0:8組卷：46引用：2難度：0.5
相似題
-
1．如圖①，以含45°的三角板的邊AB所在的直線為x軸，AB邊上的高所的直線為y軸建立平面直角坐標系．已知點A（-6，0），B（6，0），C（0，6）．E是線段AB上的動點，BF⊥CE于點F，并交y軸于點G．
（1）若∠1=20°，求∠2的度數；
（2）求證：△AEC≌△CGB．
（3）如圖圖②直線AH垂直于CE，垂足為H，并交y軸于點M．點E從A點出發，以每秒2個單位的速度向右運動，當運動時間為t秒（0≤t＜6）時，請用含t的式子表示點M的坐標．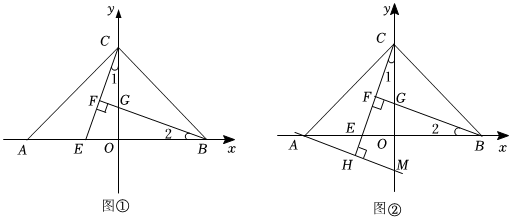
發布：2025/6/12 19:0:1組卷：9引用：1難度：0.3 -
2．如圖1，在△ABC和△ADE中，∠DAE=∠BAC，AD=AE，AB=AC．
（1）求證：△ABD≌△ACE；
（2）如圖2，在△ABC和△ADE中，∠DAE=∠BAC，AD=AE，AB=AC，∠ADB=90°，點E在△ABC內，延長DE交BC于點F，求證：點F是BC中點；
（3）△ABC為等腰三角形，∠BAC=120°，AB=AC，點P為△ABC所在平面內一點，∠APB=120°，AP=2，BP=4，求CP的長．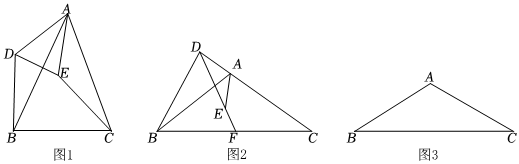
發布：2025/6/12 13:30:2組卷：414引用：2難度：0.4 -
3．如圖，在平面直角坐標系中，已知，點A（0，a），B（b,0），C（0，c），a,b,c滿足（a-8）2+|2b-12|=-
，c+2
（1）直接寫出點A，B，C的坐標及△ABC的面積；
（2）如圖2，過點C作直線l∥AB，已知D（m,n）是l上的一點且滿足4m+3n=-6，且S△ACD≤，求n的取值范圍；152
（3）如圖3，M（x,y）是線段AB上一點，
①求x,y之間的關系；
②若點N向左平移2x個單位，且S△BCN=21，求點M的坐標．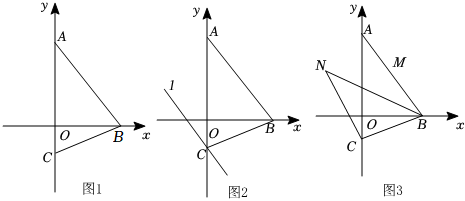
發布：2025/6/12 13:30:2組卷：38引用：1難度：0.2