閱讀理解：對于任意正實數a,b
∵（a-b）2≥0，
∴a-2ab+b≥0，∴a+b≥2ab，
∴當a=b時，a+b有最小值2ab．
根據上述內容，回答下列問題
（1）若m＞0，只有當m=11時，m+1m有最小值 22；
若m＞0，只有當m=22時，2m+8m有最小值 88；
（2）疫情需要為解決臨時隔離問題，檢測人員利用一面墻（墻的長度不限）和63米長的鋼絲網圍成了9間相同的矩形隔離房，如圖設每間隔離房的面積為S（米2）．問：當每間隔離房的長寬各為多少時，使每間隔離房面積S最大？最大面積是多少？
（
a
-
b
）
2
≥
0
a
-
2
ab
+
b
≥
0
a
+
b
≥
2
ab
2
ab
m
+
1
m
2
m
+
8
m
【考點】二次函數的應用．
【答案】1；2；2；8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：183引用：2難度：0.5
相似題
-
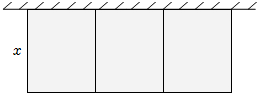1．如圖，在一面靠墻的空地上用長為24米的籬笆，圍成中間隔有二道籬笆的長方形花圃．設垂直于墻的一面籬笆長為x米，花圃的總面積為S平方米．
（1）若圍成花圃的總面積為20平方米，請設計方案．
（2）求S關于x的函數關系式，并求出最大面積．發布：2025/6/12 16:0:1組卷：115引用：7難度：0.6 -
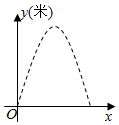2．某廣場有一噴水池，水從地面噴出，如圖，以水平地面為x軸，出水點為原點，建立平面直角坐標系，水在空中劃出的曲線是拋物線y=-2x2+4x（單位：米）的一部分，則水噴出的最大高度是 米．發布：2025/6/12 16:30:2組卷：402引用：5難度：0.6 -
3．某商品的進價為每件30元，當售價為每件40元時，每個月可賣230件．如果每件商品的售價每上漲1元，則每個月少賣10件．規定每件售價不能高于55元，設每件商品的售價上漲x元（x為正整數），每個月的銷售利潤為y元．
（1）求y與x之間的函數關系式，并寫出自變量的取值范圍；
（2）每件商品的售價定為多少時，每個月可獲得最大利潤？最大月利潤是多少元？
（3）若在銷售過程中，每件商品都有a（a＞1）元的其它費用，商家發現，當售價每件不低于49元時，每月的銷售利潤隨x的增大而減小．求a的取值范圍．發布：2025/6/12 15:30:1組卷：206引用：1難度：0.4