十八世紀(jì)瑞士數(shù)學(xué)家歐拉證明了簡單多面體中頂點(diǎn)數(shù)(V)、面數(shù)(F)、棱數(shù)(E)之間存在的一個(gè)有趣的關(guān)系式,被稱為歐拉公式.
請你觀察下列幾種簡單多面體模型,解答下列問題:
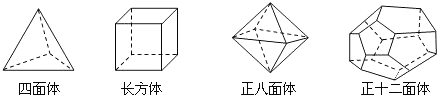
(1)根據(jù)上面多面體模型,完成表格中的空格:
| 多面體 | 頂點(diǎn)數(shù)(V) | 面數(shù)(F) | 棱數(shù)(E) |
| 四面體 | 4 | 4 |
6 6
|
| 長方體 | 8 | 6 | 12 |
| 正八面體 |
6 6
|
8 | 12 |
| 正十二面體 | 20 | 12 | 30 |
V+F-E=2
V+F-E=2
.(2)一個(gè)多面體的面數(shù)比頂點(diǎn)數(shù)大8,且有30條棱,則這個(gè)多面體的面數(shù)是
20
20
.(3)某個(gè)玻璃飾品的外形是簡單多面體,它的外表面是由三角形和八邊形兩種多邊形拼接而成,且有24個(gè)頂點(diǎn),每個(gè)頂點(diǎn)處都有3條棱,設(shè)該多面體外表面三角形的個(gè)數(shù)為x個(gè),八邊形的個(gè)數(shù)為y個(gè),求x+y的值.
【考點(diǎn)】歐拉公式.
【答案】6;6;V+F-E=2;20
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:89引用:38難度:0.7
相似題
-
1.圖1(1)、(2)、(3)依次表示四面體、八面體、正方體.
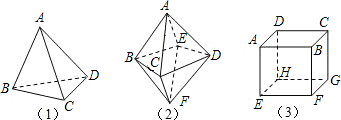
它們各自的面積數(shù)F、棱數(shù)E與頂點(diǎn)數(shù)V如下表:
觀察這些數(shù)據(jù),可以發(fā)現(xiàn)F、E、V之間的關(guān)系滿足等式:.F E V 四面體 4 6 4 八面體 8 12 6 正方體 6 12 8 發(fā)布:2025/5/26 14:0:2組卷:107引用:1難度:0.5 -
2.十八世紀(jì)瑞士數(shù)學(xué)家歐拉證明了簡單多面體中頂點(diǎn)數(shù)(V)、面數(shù)(F)、棱數(shù)(E)之間存在的一個(gè)有趣的關(guān)系式,被稱為歐拉公式.請你觀察下列幾種簡單多面體模型,解答下列問題:
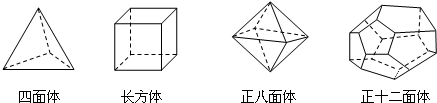
(1)根據(jù)上面多面體模型,完成表格中的空格:
你發(fā)現(xiàn)頂點(diǎn)數(shù)(V)、面數(shù)(F)、棱數(shù)(E)之間存在的關(guān)系式是 .多面體 頂點(diǎn)數(shù)(V) 面數(shù)(F) 棱數(shù)(E) 四面體 長方體 正八面體 正十二面體
(2)一個(gè)多面體的面數(shù)比頂點(diǎn)數(shù)小8,且有30條棱,則這個(gè)多面體的面數(shù)是 .
(3)某個(gè)玻璃飾品的外形是簡單多面體,它的外表面是由三角形和八邊形兩種多邊形拼接而成,且有24個(gè)頂點(diǎn),每個(gè)頂點(diǎn)處都有3條棱,設(shè)該多面體外表面三角形的個(gè)數(shù)為x個(gè),八邊形的個(gè)數(shù)為y個(gè),求x+y的值.發(fā)布:2024/9/15 8:0:8組卷:529引用:4難度:0.5 -
3.正多面體共有五種,它們是 、、、、,它們的面數(shù)f,棱數(shù)e、頂點(diǎn)數(shù)v滿足關(guān)系式 .
發(fā)布:2025/5/28 2:0:5組卷:67引用:1難度:0.5


