點P在四邊形ABCD的對角線AC上，直角三角板PEF繞直角頂點P旋轉，其邊PE、PF分別交BC、CD邊于點M、N．
（1）【操作發現】
如圖①，若四邊形ABCD是正方形，當PM⊥BC時，可知四邊形PMCN是正方形，顯然PM=PN．當PM與BC不垂直時，判斷確定PM、PN之間的數量關系； PM=PNPM=PN．（直接寫出結論即可）
（2）【類比探究】
如圖②，若四邊形ABCD是矩形，試說明PMPN=ABAD．
（3）【拓展應用】
如圖③，改變四邊形ABCD、△PEF的形狀，使四邊形ABCD內接于圓，其他條件不變，且滿足AB=8，AD=6，∠EPF=∠BAD＞90°時，求PMPN的值．
PM
PN
=
AB
AD
PM
PN
【考點】圓的綜合題．
【答案】PM=PN
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/22 3:0:1組卷：206引用：2難度：0.1
相似題
-
1．閱讀與思考
下面是一篇數學小論文，請仔細閱讀并完成相應的任務．
“三點共線模型”及其應用
背景知識：通過初中學習，我們掌握了基本事實：兩點之間線段最短．根據這個事實，我們證明了：三角形兩邊的和大于第三邊．根據不等式的性質得出了：三角形兩邊的差小于第三邊．
知識拓展：如圖，在同一平面內，已知點A和B為定點，點C為動點，且BC為定長（令BC＜AB），可得線段AB的長度為定值．我們探究AC和兩條定長線段AB，BC的數量關系及其最大值和最小值：當動點C不在直線AB上時，如圖1，由背景知識，可得結論AB+BC＞AC，AB-BC＜AC．
當動點C在直線AB上時，出現圖2和圖3兩種情況．在圖2中，線段AC取最小值為AB-BC；在圖3中，線段AC取最大值為AB+BC．
模型建立：在同一平面內，點A和B為定點，點C為動點，且AB，BC為定長（BC＜AB），則有結論AB+BC≥AC，AB-BC≤AC．當且僅當點B運動至A，C，B三點共線時等成立．
我們稱上述模型為“三點共線模型”，運用這個模型可以巧妙地解決一些最值問題．
任務：
（1）上面小論文中的知識拓展部分．主要運用的數學思想有 ；（填選項）
A．方程思想
B．統計思想
C．分類討論
D．函數思想
（2）已知線段AB=10cm,點C為任意一點，那么線段AC和BC的長度的和的最小是 cm；
（3）已知⊙O的直徑為2cm,點A為⊙O上一點，點B為平面內任意一點，且OB=1cm,則AB的最大值是 cm；
（4）如圖4，∠MON=90°，矩形ABCD的頂點A、B分別在邊OM、ON上，當B在ON邊上運動時，A隨之在OM上運動，矩形ABCD的形狀保持不變．其中AB=2，BC=1．運動過程中，求點D到點O的最大距離．發布：2025/5/22 22:30:1組卷：375引用：2難度：0.5 -
2．旋轉的圖形帶來結論的奧秘．已知△ABC，將△ABC繞點A逆時針旋轉得到△AB'C'．
初步探索 素材1： 
如圖①，連接對應點BB'，CC'，則．BB′CC′=ABAC素材2： 
如圖②，以A為圓心，BC邊上的高AD為半徑作⊙A，則B'C'與⊙A相切．問題解決 （1）（ⅰ）請證明素材1所發現的結論．
（ⅱ）如圖2，過點A作AD'⊥B'C'，垂足為D'．證明途徑可以用下面的框圖表示，請填寫其中的空格．
深入研究 （2）在Rt△ABC滿足∠A=90°， ，AB=5，M是AC的中點，△ABC繞點M逆時針旋轉得△A'B'C'．AC=25
（ⅰ）如圖③，當邊B'C'恰好經過點C時，連接BB'，則BB'的長為 ．
（ⅱ）若邊B'C'所在直線l恰好經過點B，于圖④中利用無刻度的直尺和圓規作出直線l.（只保留作圖痕跡）
（3）在（2）的條件下，如圖⑤，在旋轉過程中，直線BB'，CC'交于點P，求BP的最大值為 ．
發布：2025/5/22 22:30:1組卷：204引用：1難度：0.1 -
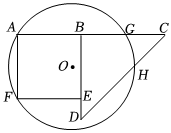3．如圖，點G在線段AC上，AG=6，點B是線段AG上一動點，以AB為邊向下方作正方形ABEF，以BC為腰向下方作等腰直角三角形BCD，∠CBD=Rt∠，當AB＜BC時，2BG-DE=4．
（1）如下表，某同學分別用特殊值法和一般法求CG的長，請你將解答過程補充完整．
（2）過點A，F，G的⊙O交邊CD于點H．探究1 假設BG=3，求CG的長． 探究2 設BG=x,求CG的長． 解：… 解：…
①連結GH，FH，若△CGH是等腰三角形，求AB的長．
②當⊙O與邊CD有兩個交點時，求AB的取值范圍．發布：2025/5/22 23:0:1組卷：463引用：3難度：0.2