閱讀與思考
下面是一篇數(shù)學(xué)小論文,請(qǐng)仔細(xì)閱讀并完成相應(yīng)的任務(wù).
“三點(diǎn)共線模型”及其應(yīng)用
背景知識(shí):通過初中學(xué)習(xí),我們掌握了基本事實(shí):兩點(diǎn)之間線段最短.根據(jù)這個(gè)事實(shí),我們證明了:三角形兩邊的和大于第三邊.根據(jù)不等式的性質(zhì)得出了:三角形兩邊的差小于第三邊.
知識(shí)拓展:如圖,在同一平面內(nèi),已知點(diǎn)A和B為定點(diǎn),點(diǎn)C為動(dòng)點(diǎn),且BC為定長(令BC<AB),可得線段AB的長度為定值.我們探究AC和兩條定長線段AB,BC的數(shù)量關(guān)系及其最大值和最小值:當(dāng)動(dòng)點(diǎn)C不在直線AB上時(shí),如圖1,由背景知識(shí),可得結(jié)論AB+BC>AC,AB-BC<AC.

當(dāng)動(dòng)點(diǎn)C在直線AB上時(shí),出現(xiàn)圖2和圖3兩種情況.在圖2中,線段AC取最小值為AB-BC;在圖3中,線段AC取最大值為AB+BC.
模型建立:在同一平面內(nèi),點(diǎn)A和B為定點(diǎn),點(diǎn)C為動(dòng)點(diǎn),且AB,BC為定長(BC<AB),則有結(jié)論AB+BC≥AC,AB-BC≤AC.當(dāng)且僅當(dāng)點(diǎn)B運(yùn)動(dòng)至A,C,B三點(diǎn)共線時(shí)等成立.
我們稱上述模型為“三點(diǎn)共線模型”,運(yùn)用這個(gè)模型可以巧妙地解決一些最值問題.
任務(wù):
(1)上面小論文中的知識(shí)拓展部分.主要運(yùn)用的數(shù)學(xué)思想有 CC;(填選項(xiàng))
A.方程思想
B.統(tǒng)計(jì)思想
C.分類討論
D.函數(shù)思想
(2)已知線段AB=10cm,點(diǎn)C為任意一點(diǎn),那么線段AC和BC的長度的和的最小是 1010cm;
(3)已知⊙O的直徑為2cm,點(diǎn)A為⊙O上一點(diǎn),點(diǎn)B為平面內(nèi)任意一點(diǎn),且OB=1cm,則AB的最大值是 22cm;
(4)如圖4,∠MON=90°,矩形ABCD的頂點(diǎn)A、B分別在邊OM、ON上,當(dāng)B在ON邊上運(yùn)動(dòng)時(shí),A隨之在OM上運(yùn)動(dòng),矩形ABCD的形狀保持不變.其中AB=2,BC=1.運(yùn)動(dòng)過程中,求點(diǎn)D到點(diǎn)O的最大距離.
【考點(diǎn)】圓的綜合題.
【答案】C;10;2
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2025/5/22 22:30:1組卷:376引用:2難度:0.5
相似題
-
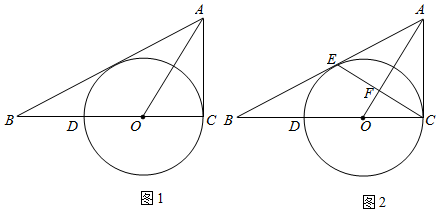
 1.如圖,已知O是△ABC邊AB上的一點(diǎn),以O(shè)為圓心、OB為半徑的⊙O與邊AC相切于點(diǎn)D,且BC=CD,連接OC,交⊙O于點(diǎn)E,連接BE并延長,交AC于點(diǎn)F.
1.如圖,已知O是△ABC邊AB上的一點(diǎn),以O(shè)為圓心、OB為半徑的⊙O與邊AC相切于點(diǎn)D,且BC=CD,連接OC,交⊙O于點(diǎn)E,連接BE并延長,交AC于點(diǎn)F.
(1)求證:BC是⊙O切線;
(2)求證:OA?AB=AD?AC;
(3)若,求EO的長.AC=10,tan∠BAC=43發(fā)布:2025/5/23 11:30:2組卷:738引用:4難度:0.3 -
2.在Rt△ABC中,∠ACB=90°,OA平分∠BAC交BC于點(diǎn)O,以O(shè)為圓心,OC長為半徑作圓交BC于點(diǎn)D.
(1)如圖1,求證:AB為⊙O的切線;
(2)如圖2,AB與⊙O相切于點(diǎn)E,連接CE交OA于點(diǎn)F.
①試判斷線段OA與CE的位置關(guān)系,并說明理由.
②若OF:FC=1:2,求tanB的值.發(fā)布:2025/5/23 12:0:2組卷:1493引用:4難度:0.5 -
3.已知平面直角坐標(biāo)系xOy中的點(diǎn)P和⊙O,⊙O的半徑是4,交x軸于點(diǎn)A,B.對(duì)于點(diǎn)P給出如下定義:過點(diǎn)C的直線與⊙O交于點(diǎn)M,N,點(diǎn)P為線段MN的中點(diǎn),我們把這樣的點(diǎn)P叫做關(guān)于MN的“弦中點(diǎn)”.
(1)如圖1,已知點(diǎn)C(-2,0);
①點(diǎn)P1(0,0),P2(-1,1),P3(2,2)中是關(guān)于MN的“弦中點(diǎn)”的是 ;
②若一次函數(shù)y=x+b的圖象上只存在一個(gè)關(guān)于MN的“弦中點(diǎn)”,求b的值;12
(2)如圖2,若C(-6,0),一次函數(shù)y=x+b的圖象上存在關(guān)于MN的“弦中點(diǎn)”,直接寫出b的取值范圍. 發(fā)布:2025/5/23 12:0:2組卷:673引用:3難度:0.3
發(fā)布:2025/5/23 12:0:2組卷:673引用:3難度:0.3
相關(guān)試卷


