某工廠研發了一種新型產品，并投放市場，已知制造成本為18元/件．經過市場調查發現，銷售單價為30元時，每月的銷售量為40（萬件）；銷售單價為20元時，每月的銷售量為60（萬件）；如果每月的銷售量y（萬件）與銷售單價x（元/件）成一次函數關系．
（1）求每月的利潤w（萬元）與銷售單價x（元件）之間的函數關系式；
（2）根據市場監管部門規定，這種產品的銷售利潤率不能高于50%，同時廠家要求這種產品每月的制造成本不能超過900萬元，當銷售單價為多少元時，廠家每月能獲得最大利潤？最大利潤是多少？
【考點】二次函數的應用．
【答案】（1）y=-2x2+136x-1800；（2）當銷售單價為27元時，廠商每月獲得的利潤最大，最大利潤為414萬元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/9 21:0:1組卷：25引用：1難度：0.6
相似題
-
1．某商店決定購A，B兩種“冰墩墩”紀念品進行銷售．已知每件A種紀念品比每件B種紀念品的進價高30元．用1000元購進A種紀念品的數量和用400元購進B種紀念品的數量相同．
（1）求A，B兩種紀念品每件的進價分別是多少元？
（2）該商場通過市場調查，整理出A型紀念品的售價與數量的關系如表，
求當x為何值時，售出A紀念品所獲利潤最大，最大利潤為多少？售價x元/件 50≤x≤60 60＜x≤80 銷售量（件） 100 400-5x 發布：2025/6/9 21:30:1組卷：256引用：3難度：0.5 -
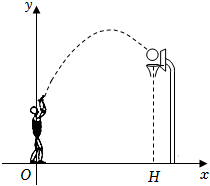2．如圖，一位籃球運動員投籃，球沿拋物線y=-0.2x2+x+2.25運行，然后準確落入籃筐內，已知籃筐的中心離地面的高度為3.05m,則他距籃筐中心的水平距離OH是 m.發布：2025/6/10 0:0:1組卷：3127引用：13難度：0.5 -
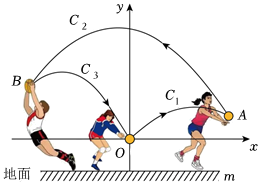3．排球考試要求：墊球后，球在運動中離地面的最大高度至少為2米．某次模擬測試中，某生在O處將球墊偏，之后又在A、B兩處先后墊球，球沿拋物線C1→C2→C3運動（假設拋物線C1、C2、C3在同一平面內），最終正好在O處墊住，O處離地面的距離為1米．如圖所示，以O為坐標原點1米為單位長度建立直角坐標系，x軸平行于地面水平直線m,已知點，點B的橫坐標為A（32，38），拋物線C1表達式為y=ax2-2ax和拋物線C3表達式為y=2ax2+bx（a≠0）．-32
（1）求拋物線C1的函數表達式；
（2）第一次墊球后，球在運動中離地面的最大高度是否達到要求？請說明理由；
（3）為了使第三次墊球后，球在運動中離地面的最大高度達到要求，該生第三次墊球處B離地面的高度至少為多少米？發布：2025/6/10 0:0:1組卷：842引用：6難度：0.4