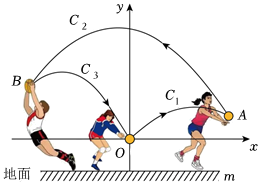
排球考試要求：墊球后，球在運動中離地面的最大高度至少為2米．某次模擬測試中，某生在O處將球墊偏，之后又在A、B兩處先后墊球，球沿拋物線C1→C2→C3運動（假設拋物線C1、C2、C3在同一平面內），最終正好在O處墊住，O處離地面的距離為1米．如圖所示，以O為坐標原點1米為單位長度建立直角坐標系，x軸平行于地面水平直線m,已知點A（32，38），點B的橫坐標為-32，拋物線C1表達式為y=ax2-2ax和拋物線C3表達式為y=2ax2+bx（a≠0）．
（1）求拋物線C1的函數表達式；
（2）第一次墊球后，球在運動中離地面的最大高度是否達到要求？請說明理由；
（3）為了使第三次墊球后，球在運動中離地面的最大高度達到要求，該生第三次墊球處B離地面的高度至少為多少米？
A
（
3
2
，
3
8
）
-
3
2
【考點】二次函數的應用．
【答案】（1）；
（2）最大高度未達到要求，理由見解析；
（3）1.75米．
y
=
-
1
2
x
2
+
x
（2）最大高度未達到要求，理由見解析；
（3）1.75米．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/10 0:0:1組卷：842引用：6難度：0.4
相似題
-
1．某商店代銷一批季節性服裝，每套代銷成本40元，第一個月每套銷售定價為52元時，可售出180套；應市場變化需上調第一個月的銷售價，預計銷售定價每增加1元，銷售量將減少10套．
（1）若設第二個月的銷售定價每套增加x元，填寫下表：
（2）若商店預計要在第二個月的銷售中獲利2000元，則第二個月銷售定價每套多少元？時間 第一個月 第二個月 銷售定價（元） 52 銷售量（套） 180
（3）若要使第二個月利潤達到最大，應定價為多少元？此時第二個月的最大利潤是多少？發布：2025/6/10 4:30:1組卷：275引用：5難度：0.3 -
2．隨著人們生活水平提升，我市市民對花卉需求量也在增加．新春佳節臨近，購買自己喜愛的鮮花裝飾家庭成為青島市民必備的時尚年貨．市民走進花卉市場，尋找春景春色，賞花買花，體驗濃濃年味．春節前夕，某花卉市場店鋪老板用5400元按批發價購買了一批花卉．若將批發價降低10%，則可以多購買該花卉20盆．據市場調查反映，該花卉每盆售價42元時，每天可賣出20盆；若調整價格，每盆花卉每漲價2元，每天要少賣出1盆．
（1）該花卉每盆批發價是多少元？
（2）店鋪老板決定在每盆售價42元的基礎上，每盆花卉漲價不超過10元，問該花卉一天最大的銷售利潤是多少元？
（3）該店鋪開展快遞托運送貨到家活動，但每盆花卉店鋪還需增加a元的快遞成本，若每盆花卉售價不低于62元時，每天的利潤將隨著售價的增長不斷降低，請直接寫出快遞成本最多是多少元？發布：2025/6/10 4:30:1組卷：792引用：2難度：0.3 -
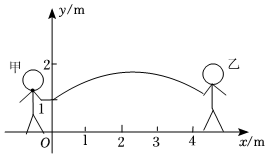3．跳繩是大家喜愛的一項體育運動，當繩子甩到最高處時，其形狀視為拋物線．如圖是甲，乙兩人將繩子甩到最高處時的示意圖，已知兩人拿繩子的手離地面的高度都為1m,并且相距4m,現以兩人的站立點所在的直線為x軸，過甲拿繩子的手作x軸的垂線為y軸，建立如圖所示的平面直角坐標系，且繩子所對應的拋物線解析式為．y=-16x2+bx+c
（1）求繩子所對應的拋物線解析式（不要求寫自變量的取值范圍）；
（2）身高1.70m的小明，能否站在繩子的正下方，讓繩子通過他的頭頂？
（3）身高1.64m的小軍，站在繩子的下方，設他距離甲拿繩子的手sm,為確保繩子能通過他的頭頂，請求出s的取值范圍．發布：2025/6/10 4:30:1組卷：611引用：6難度：0.6