某企業設計了一款工藝品，每件的成本是50元，為了合理定價，投放市場進行試銷．據市場調查，銷售單價是100元時，每天的銷售量是50件，而銷售單價每降低1元，每天就可多售出5件，但要求銷售單價不得低于成本．
（1）求出每天的銷售利潤y（元）與銷售單價x（元）之間的函數關系式；
（2）求出銷售單價為多少元時，每天的銷售利潤最大？最大利潤是多少？
（3）如果該企業要使每天的銷售利潤不低于4000元，那么銷售單價應控制在什么范圍內？
【考點】二次函數的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/28 3:0:8組卷：3057引用：22難度：0.5
相似題
-
1．晨光中學課外活動小組準備圍建一個矩形生物苗圃園，其中一邊靠墻，另外三邊用長為30米的籬笆圍成．已知墻長為18米（如圖所示），設這個苗圃園垂直于墻的一邊的長為x米．
（1）設這個苗圃園的面積為S，求S與x之間的函數關系，并直接其自變量x的取值范圍；
（2）當矩形場地的面積為100m2時，求垂直于墻的一邊的長．發布：2025/5/22 8:30:1組卷：698引用：2難度：0.8 -
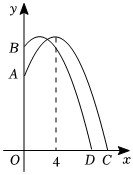2．為了有效地應對高樓火災，某消防中隊進行消防技能比賽．如圖，在一個廢棄高樓距地面10m的點A和15m的點B處，各設置了一個火源，消防員來到火源正前方，水槍噴出的水流看作拋物線的一部分（水流出口與地面的距離忽略不計）．第一次滅火時站在水平地面的點C處，水流恰好到達點A處，且水流的最大高度為16m,水流的最高點到高樓的水平距離為4m,建立如圖所示的平面直角坐標系，水流的高度y（m）與到高樓的水平距離x（m）之間的函數關系式為：y=a（x-h）2+k.
（1）求消防員第一次滅火時水流所在拋物線的解析式；
（2）待A處火熄滅后，消防員前進2m到點D處進行第二次滅火，若兩次滅火時水流所在拋物線的形狀相同，請判斷水流是否到達點B處，并說明理由；
（3）若消防員站在到高樓的水平距離為11m～12m的地方，調整水槍，使噴出的水流形狀發生變化，水流的最高點到高樓的水平距離始終是4m,當時，求水流到達墻面高度的取值范圍．-12≤a≤-13發布：2025/5/22 8:0:2組卷：612引用：4難度：0.5 -
3．某景區有兩個景點需購票游覽，售票處出示的三種購票方式如下：
方式1：只購買景點A，30元/人；
方式2：只購買景點B，50元/人；
方式3：景點A和B聯票，70元/人．
預測，四月份選擇這三種購票方式的人數分別有2萬、1萬和1萬．為增加收入，對門票價格進行調整，發現當方式1和2的門票價格不變時，方式3的聯票價格每下降1元，將有原計劃只購買A門票的400人和原計劃只購買B門票的600人改為購買聯票．
（1）若聯票價格下降5元，則購買方式1門票的人數有 萬人，購買方式2門票的人數有 萬人，購買方式3門票的人數有 萬人；并計算門票總收入有多少萬元？
（2）當聯票價格下降x（元）時，請求出四月份的門票總收入w（萬元）與x（元）之間的函數關系式，并求出聯票價格為多少元時，四月份的門票總收入最大？最大值是多少萬元？發布：2025/5/22 8:0:2組卷：442引用：5難度：0.5