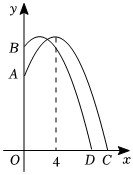
為了有效地應對高樓火災，某消防中隊進行消防技能比賽．如圖，在一個廢棄高樓距地面10m的點A和15m的點B處，各設置了一個火源，消防員來到火源正前方，水槍噴出的水流看作拋物線的一部分（水流出口與地面的距離忽略不計）．第一次滅火時站在水平地面的點C處，水流恰好到達點A處，且水流的最大高度為16m,水流的最高點到高樓的水平距離為4m,建立如圖所示的平面直角坐標系，水流的高度y（m）與到高樓的水平距離x（m）之間的函數關系式為：y=a（x-h）2+k.
（1）求消防員第一次滅火時水流所在拋物線的解析式；
（2）待A處火熄滅后，消防員前進2m到點D處進行第二次滅火，若兩次滅火時水流所在拋物線的形狀相同，請判斷水流是否到達點B處，并說明理由；
（3）若消防員站在到高樓的水平距離為11m～12m的地方，調整水槍，使噴出的水流形狀發(fā)生變化，水流的最高點到高樓的水平距離始終是4m,當-12≤a≤-13時，求水流到達墻面高度的取值范圍．
-
1
2
≤
a
≤
-
1
3
【考點】二次函數的應用．
【答案】（1）；
（2）不能，理由見解析；
（3）11≤d≤24．
y
=
-
3
8
（
x
-
4
）
2
+
16
（2）不能，理由見解析；
（3）11≤d≤24．
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2025/5/22 8:0:2組卷：612引用：4難度：0.5
相似題
-
1．鉛球運動員在比賽時，鉛球被擲出后的運動路線可以看作是拋物線的一部分．在某次比賽的一次投擲過程中，鉛球被擲出后，設鉛球距運動員出手點的水平距離為x（單位：m），豎直高度為y（單位：m）．由電子監(jiān)測獲得的部分數據如下：
（1）根據上述數據，直接寫出鉛球豎直高度的最大值，并求出滿足的函數關系y=a（x-h）2+k（a＜0）；水平距離x/m 0 3 6 9 12 15 18 … 豎直高度y/m 2.00 4.25 5.60 6.05 5.60 4.25 2.00 …
（2）請你建立平面直角坐標系，描出上表中各對對應值為坐標的點，畫出y與x的函數圖象；
（3）請你結合所畫圖象或所求函數關系式，直接寫出本次投擲后，鉛球距運動員出手點的最遠水平距離．發(fā)布：2025/5/22 14:30:2組卷：284引用：1難度：0.6 -
2．“愛成都，創(chuàng)文明，迎大運”，衛(wèi)生環(huán)境先著手，為提高工作效率，某清潔工具生產商投產一種新型垃圾夾，每件制造成本為20元，在試銷過程中發(fā)現，每月銷量y（萬件）與銷售單價x（元）之間關系可以近似地看作一次函數y=-2x+52．
（1）寫出每月的利潤w（萬元）與銷售單價x（元）之間函數解析式；
（2）當銷售單價為多少元時，生產商每月能夠獲得最大利潤？最大利潤是多少？發(fā)布：2025/5/22 14:0:1組卷：369引用：2難度：0.6 -
3．如圖，不考慮空氣阻力，以一定的速度將小球沿斜上方擊出時，小球飛行的高度是飛行時間的二次函數．現以相同的初速度沿相同的方向每隔t秒依次擊出三個質地一樣的小球，小球在各自擊出后1秒到達相同的最大飛行高度，若整個過程中同時出現在空中的小球個數最大值為2（不考慮小球落地后再彈起），則t的取值范圍是（ ）發(fā)布：2025/5/22 14:30:2組卷：386引用：2難度：0.5