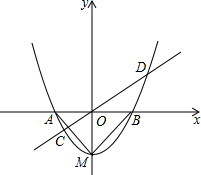
如圖，已知拋物線y=x2+bx+c的頂點坐標為M（0，-1），與x軸交于A、B兩點．
（1）求拋物線的解析式；
（2）判斷△MAB的形狀，并說明理由；
（3）過原點的任意直線（不與y軸重合）交拋物線于C、D兩點，連接MC，MD，試判斷MC、MD是否垂直，并說明理由．
【考點】二次函數綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：2343引用：56難度：0.1
相似題
-
1．拋物線y=x2-2x-3交x軸于A，B兩點（A在B的左邊），C是第一象限拋物線上一點，直線AC交y軸于點P．
（1）直接寫出A，B兩點的坐標；
（2）如圖（1），當OP=OA時，在拋物線上存在點D（異于點B），使B，D兩點到AC的距離相等，求出所有滿足條件的點D的橫坐標；
（3）如圖（2），直線BP交拋物線于另一點E，連接CE交y軸于點F，點C的橫坐標為m.求的值（用含m的式子表示）．FPOP
發布：2025/5/21 12:0:1組卷：351引用：1難度：0.3 -
2．已知，拋物線L：y=x2-4mx（m≠0），直線x=m將拋物線L分成兩部分，首先去掉其不含頂點的部分，然后作出拋物線剩余部分關于直線x=m的對稱圖形，得到的整個圖形L′稱為拋物線L關于直線x=m的“L雙拋圖形”；
感知特例
如圖所示，當m=1時，拋物線L：y=x2-4mx上的點B，C，A，D，E分別關于直線x=m對稱的點為B′，C′，A′，D′，E′如下表：
①補全表格；… B（1，-3） C（2，-4） A（3，-3） D（4，0） E（5，5） … … B′（1，-3） C′（ ，） A′（ ，） D′（-2，0） E′（-3，5） …
②在圖中描出表中對稱點，再用平滑的曲線依次連接各點，得到圖象記為L′；
③若雙拋圖形L′與直線y=t恰好有三個交點，則t的值為 ；
④若雙拋圖形L′的函數值隨著x的增大而增大，則x的取值范圍為 ；
探究問題
（2）①若雙拋圖形L′與直線y=t恰好有三個交點，則t的值為 ；（用含m的式子表達）
②若雙拋圖形L′的函數值隨著x的增大而增大，直接寫出x的取值范圍；（用含m的式子表達）
③拋物線L的頂點為點C，點C關于直線x=m對稱點為C′，直線x=m與雙拋圖形L′交點為點B，若△BCC′為等邊三角形時，求m的值．發布：2025/5/21 12:0:1組卷：349引用：1難度：0.3 -
3．定義：若拋物線y=ax2+bx+c（ac≠0）與x軸交于A，B兩點，與y軸交于點C．線段OA，OB，OC的長滿足OC2=OA?OB，則這樣的拋物線稱為“黃金拋物線”．如圖，“黃金拋物線”y=ax2+bx+2（a≠0）與x軸的負半軸交于點A，與x軸的正半軸交于點B，與y軸交于點C，且OA=4OB．
（1）求拋物線的解析式；
（2）點P為AC上方拋物線上的動點，過點P作PD⊥AC于點D．
①求PD的最大值；
②連接PC，當以點P，C，D為頂點的三角形與△A CO相似時，求點P的坐標．
發布：2025/5/21 12:0:1組卷：297引用：1難度：0.3