人教五四新版九年級（上）中考題單元試卷：第28章 二次函數（24）

一、解答題（共30小題）

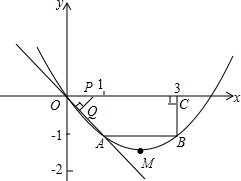• 1．已知：如圖，在四邊形OABC中，AB∥OC，BC⊥x軸于點C，A（1，-1），B（3，-1），動點P從點O出發，沿著x軸正方向以每秒2個單位長度的速度移動．過點P作PQ垂直于直線OA，垂足為點Q，設點P移動的時間t秒（0＜t＜2），△OPQ與四邊形OABC重疊部分的面積為S．
  （1）求經過O、A、B三點的拋物線的解析式，并確定頂點M的坐標；
  （2）用含t的代數式表示點P、點Q的坐標；
  （3）如果將△OPQ繞著點P按逆時針方向旋轉90°，是否存在t,使得△OPQ的頂點O或頂點Q在拋物線上？若存在，請求出t的值；若不存在，請說明理由；
  （4）求出S與t的函數關系式．
  組卷：3884引用：61難度：0.1

  解析

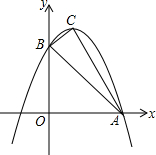• 2．如圖，已知拋物線y=ax²+bx+c與x軸的一個交點為A（3，0），與y軸的交點為B（0，3），其頂點為C，對稱軸為直線x=1．
  （1）求拋物線的解析式；
  （2）已知點M為y軸上的一個動點，當△ABM為等腰三角形時，求點M的坐標；
  （3）將△AOB沿x軸向右平移m個單位長度（0＜m＜3）得到另一個三角形，將所得的三角形與△ABC重疊部分的面積記為S，用m的代數式表示S．
  組卷：3583引用：62難度：0.1

  解析

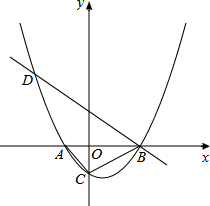• 3．如圖，已知拋物線y=

  k

  8

  （x+2）（x-4）（k為常數，且k＞0）與x軸從左至右依次交于A，B兩點，與y軸交于點C，經過點B的直線y=-

  3

  3

  x+b與拋物線的另一交點為D．
  （1）若點D的橫坐標為-5，求拋物線的函數表達式；
  （2）若在第一象限內的拋物線上有點P，使得以A，B，P為頂點的三角形與△ABC相似，求k的值；
  （3）在（1）的條件下，設F為線段BD上一點（不含端點），連接AF，一動點M從點A出發，沿線段AF以每秒1個單位的速度運動到F，再沿線段FD以每秒2個單位的速度運動到D后停止，當點F的坐標是多少時，點M在整個運動過程中用時最少？
  組卷：9688引用：70難度：0.1

  解析

• 4．如圖，在平面直角坐標系中，拋物線y=ax²+bx-3（a≠0）與x軸交于點A（-2，0）、B（4，0）兩點，與y軸交于點C．
  （1）求拋物線的解析式；
  （2）點P從A點出發，在線段AB上以每秒3個單位長度的速度向B點運動，同時點Q從B點出發，在線段BC上以每秒1個單位長度的速度向C點運動，其中一個點到達終點時，另一個點也停止運動，當△PBQ存在時，求運動多少秒使△PBQ的面積最大，最大面積是多少？
  （3）當△PBQ的面積最大時，在BC下方的拋物線上存在點K，使S_△CBK：S_△PBQ=5：2，求K點坐標．
  組卷：5718引用：69難度：0.1

  解析

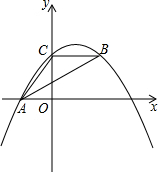• 5．如圖，拋物線y=ax²+bx+c經過A（-3，0）、C（0，4），點B在拋物線上，CB∥x軸，且AB平分∠CAO．
  （1）求拋物線的解析式；
  （2）線段AB上有一動點P，過點P作y軸的平行線，交拋物線于點Q，求線段PQ的最大值；
  （3）拋物線的對稱軸上是否存在點M，使△ABM是以AB為直角邊的直角三角形？如果存在，求出點M的坐標；如果不存在，說明理由．
  組卷：4917引用：62難度：0.1

  解析

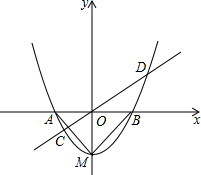• 6．如圖，已知拋物線y=x²+bx+c的頂點坐標為M（0，-1），與x軸交于A、B兩點．
  （1）求拋物線的解析式；
  （2）判斷△MAB的形狀，并說明理由；
  （3）過原點的任意直線（不與y軸重合）交拋物線于C、D兩點，連接MC，MD，試判斷MC、MD是否垂直，并說明理由．
  組卷：2343引用：56難度：0.1

  解析

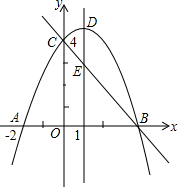• 7．如圖，拋物線y=ax²+bx+c（a≠0）與y軸交于點C（0，4），與x軸交于點A和點B，其中點A的坐標為（-2，0），拋物線的對稱軸x=1與拋物線交于點D，與直線BC交于點E．
  （1）求拋物線的解析式；
  （2）若點F是直線BC上方的拋物線上的一個動點，是否存在點F使四邊形ABFC的面積為17，若存在，求出點F的坐標；若不存在，請說明理由；
  （3）平行于DE的一條動直線l與直線BC相交于點P，與拋物線相交于點Q，若以D、E、P、Q為頂點的四邊形是平行四邊形，求點P的坐標．
  組卷：5311引用：67難度：0.1

  解析

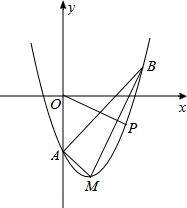• 8．如圖，在平面直角坐標系xOy中，頂點為M的拋物線是由拋物線y=x²-3向右平移一個單位后得到的，它與y軸負半軸交于點A，點B在該拋物線上，且橫坐標為3．
  （1）求點M、A、B坐標；
  （2）連接AB、AM、BM，求∠ABM的正切值；
  （3）點P是頂點為M的拋物線上一點，且位于對稱軸的右側，設PO與x軸正半軸的夾角為α，當α=∠ABM時，求P點坐標．
  組卷：4692引用：54難度：0.1

  解析

• 9．如圖①，直線l：y=mx+n（m＜0，n＞0）與x,y軸分別相交于A，B兩點，將△AOB繞點O逆時針旋轉90°得到△COD，過點A，B，D的拋物線P叫做l的關聯拋物線，而l叫做P的關聯直線．
  （1）若l：y=-2x+2，則P表示的函數解析式為

  ；若P：y=-x²-3x+4，則l表示的函數解析式為

  ．
  （2）求P的對稱軸（用含m,n的代數式表示）；
  （3）如圖②，若l：y=-2x+4，P的對稱軸與CD相交于點E，點F在l上，點Q在P的對稱軸上．當以點C，E，Q，F為頂點的四邊形是以CE為一邊的平行四邊形時，求點Q的坐標；
  （4）如圖③，若l：y=mx-4m,G為AB中點，H為CD中點，連接GH，M為GH中點，連接OM．若OM=

  10

  ，直接寫出l,P表示的函數解析式．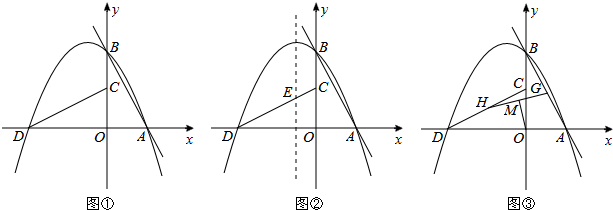
  
  組卷：4045引用：56難度：0.1

  解析

• 10．如圖，在平面直角坐標系中，已知點A的坐標是（4，0），并且OA=OC=4OB，動點P在過A，B，C三點的拋物線上．
  （1）求拋物線的解析式；
  （2）是否存在點P，使得△ACP是以AC為直角邊的直角三角形？若存在，求出所有符合條件的點P的坐標；若不存在，說明理由；
  （3）過動點P作PE垂直于y軸于點E，交直線AC于點D，過點D作x軸的垂線．垂足為F，連接EF，當線段EF的長度最短時，求出點P的坐標．
  
  組卷：5200引用：61難度：0.1

  解析

一、解答題（共30小題）

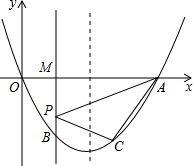• 29．如圖，拋物線y=x²-2mx（m＞0）與x軸的另一個交點為A，過P（1，-m）作PM⊥x軸于點M，交拋物線于點B．點B關于拋物線對稱軸的對稱點為C．
  （1）若m=2，求點A和點C的坐標；
  （2）令m＞1，連接CA，若△ACP為直角三角形，求m的值；
  （3）在坐標軸上是否存在點E，使得△PEC是以P為直角頂點的等腰直角三角形？若存在，求出點E的坐標；若不存在，請說明理由．
  組卷：2121引用：53難度：0.1

  解析

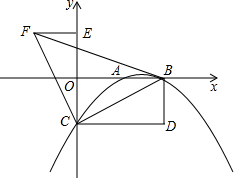• 30．如圖，拋物線y=-

  1

  4

  x²+

  3

  2

  x-2交x軸于A，B兩點（點A在點B的左側），交y軸于點C，分別過點B，C作y軸，x軸的平行線，兩平行線交于點D，將△BDC繞點C逆時針旋轉，使點D旋轉到y軸上得到△FEC，連接BF．
  （1）求點B，C所在直線的函數解析式；
  （2）求△BCF的面積；
  （3）在線段BC上是否存在點P，使得以點P，A，B為頂點的三角形與△BOC相似？若存在，求出點P的坐標；若不存在，請說明理由．
  組卷：2235引用：52難度：0.1

  解析