在矩形ABCD中，AB=3，AD=4，點E是邊AD上一點，EM⊥EC交AB于點M，點N在射線MB上，且∠ANE=∠DCE．
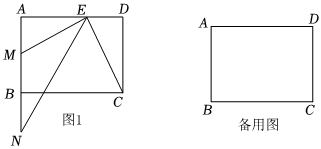
（1）如圖，求證：AE是AM和AN的比例中項；
（2）當點N在線段AB的延長線上時，聯結AC，且AC與NE互相垂直，求MN的長．
【考點】相似三角形的判定與性質；矩形的性質．
【答案】（1）證明見解析；（2）．
49
48
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 8:0:2組卷：274引用：1難度：0.5
相似題
-
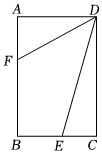1．如圖，矩形ABCD中，AB=16，BC=12，E為BC邊的中點，點F在邊AB上，∠EDF=45°，則AF的長為 ．發布：2025/6/6 7:0:2組卷：520引用：5難度：0.6 -
2．閱讀下列材料并完成相應的任務
等面積法是一種常用的、重要的數學解題方法．它是利用“同一個圖形的面積相等”、“分割圖形后各部分的面積之和等于原圖形的面積”、“同底等高或等底同高的兩個三角形面積相等”等性質解決有關數學問題．在解題中，靈活運用等面積法解決相關問題，可以使解題思路清晰，解題過程簡便快捷．
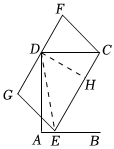
如圖，矩形ABCD的邊AB上有一動點E，以EC為邊作平行四邊形ECFG，且邊FG過矩形的頂點D，在點E從點A移動到點B的過程中，平行四邊形ECFG的面積如何變化？
小亮的觀點：過點D作DH⊥CE于點H，連接DE，CE與DH的乘積始終等于CD?AD，所以平行四邊形ECFG的面積不變．
小明的觀點：在點E的運動過程中，CE的長度在變化，而CE與FG兩條平行線間的距離不變，所以平行四邊形ECFG的面積變化．
任務：你認為小亮和小明誰的觀點正確？正確的寫出完整的證明過程．發布：2025/6/6 8:30:1組卷：35引用：1難度：0.5 -
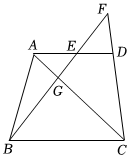3．如圖，梯形ABCD中，AD∥BC，點E是邊AD的中點，連接BE并延長交CD的延長線于點F，交AC于點G．
（1）若FD=2，，求線段DC的長；EDBC=13
（2）求證：EF?GB=BF?GE．發布：2025/6/6 6:30:1組卷：552引用：6難度：0.3