我市某童裝專賣店在銷售中發(fā)現(xiàn)，一款童裝每件進價為40元，若銷售價為60元，每天可售出20件，為迎接“雙十一”，專賣店決定采取適當?shù)慕祪r措施，以擴大銷售量，經市場調查發(fā)現(xiàn)，如果每件童裝降價1元，那么平均可多售出2件．設每件童裝降價x元（x＞0）時，平均每天可盈利y元．
（1）寫出y與x的函數(shù)關系式；
（2）當該專賣店每件童裝降價多少元時，平均每天盈利400元？
（3）當該專賣店每件童裝降價多少元時，平均每天盈利最大，并求出最大利潤？
【考點】二次函數(shù)的應用；一元二次方程的應用．
【答案】（1）y=-2x2+20x+400；（2）當該專賣店每件童裝降價10元時，平均每天盈利400元；（3）當該專賣店每件童裝降價5元時，平均每天盈利最大，最大利潤為450元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/10/4 1:0:1組卷：17引用：2難度：0.5
相似題
-
1．某果園計劃在40畝空地上全部種植蘋果和梨，種植蘋果面積大于種植梨面積，且均為整數(shù)，果農小王和小李分別承包了種植蘋果和梨的任務．
果農小王種植每畝蘋果的工資y（元）與種植面積x（畝）之間的函數(shù)關系為y=-2x+200；小李種植梨所得報酬t（元）與種植面積m（畝）之間的函數(shù)關系為t=120m+300．
（1）若小王種植蘋果為x畝，用含x的代數(shù)式表示下列各量：
①小李種植梨的面積為 畝；
②小王種植蘋果所得的總工資為 元；
③小李種植梨所得的報酬為 元；
（2）若果園支付小王和小李的總費用為5700元，求小王與小李種植的面積各為多少畝？
（3）直接寫出果園支付給小王和小李的總費用的最大值．發(fā)布：2025/5/25 0:30:1組卷：67引用：1難度：0.5 -
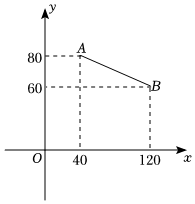2．某時令水果上市的時候，一果農以“線上”與“線下”相結合的方式一共銷售了200箱該種水果．已知“線上”銷售的每箱利潤為50元．“線下”銷售的每箱利潤y（元）與銷售量x（箱）之間的函數(shù)關系如圖中線段AB．
（1）若“線上”與“線下”銷售量相同，求果農售完這200箱水果獲得的總利潤；
（2）當“線下”的銷售利潤為4500元時，求“線下”的銷售量；
（3）實際“線下”銷售時，每箱還要支出其它相關費用m元（0＜m＜10），若“線上”與“線下”售完這200箱該水果所獲得的最大總利潤為11225元，求m的值．發(fā)布：2025/5/25 1:0:1組卷：143引用：4難度：0.4 -
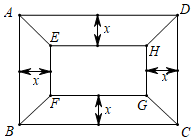3．有一塊矩形地塊ABCD，AB=20米，BC=30米．為美觀，擬種植不同的花卉，如圖所示，將矩形ABCD分割成四個等腰梯形及一個矩形，其中梯形的高相等，均為x米．現(xiàn)決定在等腰梯形AEHD和BCGF中種植甲種花卉；在等腰梯形ABFE和CDHG中種植乙種花卉；在矩形EFGH中種植丙種花卉．甲、乙、丙三種花卉的種植成本分別為20元/米2、60元/米2、40元/米2，設三種花卉的種植總成本為y元．
（1）當x=5時，求種植總成本y；
（2）求種植總成本y與x的函數(shù)表達式，并寫出自變量x的取值范圍；
（3）若甲、乙兩種花卉的種植面積之差不超過120平方米，求三種花卉的最低種植總成本．發(fā)布：2025/5/25 1:0:1組卷：2658引用：3難度：0.4