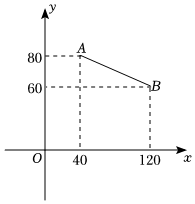
某時令水果上市的時候，一果農以“線上”與“線下”相結合的方式一共銷售了200箱該種水果．已知“線上”銷售的每箱利潤為50元．“線下”銷售的每箱利潤y（元）與銷售量x（箱）之間的函數關系如圖中線段AB．
（1）若“線上”與“線下”銷售量相同，求果農售完這200箱水果獲得的總利潤；
（2）當“線下”的銷售利潤為4500元時，求“線下”的銷售量；
（3）實際“線下”銷售時，每箱還要支出其它相關費用m元（0＜m＜10），若“線上”與“線下”售完這200箱該水果所獲得的最大總利潤為11225元，求m的值．
【考點】二次函數的應用．
【答案】（1）線上”與“線下”總利潤為11500元；
（2）“線下”的銷售量為60箱；
（3）m=5．
（2）“線下”的銷售量為60箱；
（3）m=5．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/25 1:0:1組卷：143引用：4難度：0.4
相似題
-
1．某城市發生疫情，第x天（1≤x≤15）新增病例y（人）如表所示：
（1）根據圖表（y與x滿足一次函數，二次函數，反比例函數中的一種），請求出y與x的函數解析式；x 1 2 3 4 … 14 15 y 2 24 46 68 … 288 310
（2）由于疫情傳染性強，第15天開始新增病例人數模型發生變化，第x天（x≥15）新增病例y（人）滿足y=-5（x-m）（x-13）（m為已知數）．請預計第幾天新增病例清零；
（3）為應對本輪疫情，按照每一個新增病例需當天提供一張病床的要求，政府應該在哪一天為新增病例提供的病床最多？最多應該提供多少張病床？發布：2025/5/25 5:30:2組卷：338引用：2難度：0.6 -
2．云浮市各級公安交警部門提醒市民，騎車出行必須嚴格遵守“一盔一帶”的規定，郁南縣某商場同時購進A，B兩種類型的頭盔，已知購進3個A類頭盔和4個B類頭盔共需288元；購進6個A類頭盔和2個B類頭盔共需306元．
（1）A，B兩類頭盔每個的進價各是多少元？
（2）在銷售中，該商場發現A類頭盔每個售價50元時，每個月可售出100個；每個售價提高5元時，每個月少售出10個．設A類頭盔每個x元（50≤x≤100），y表示該商家每月銷售A類頭盔的利潤（單位：元），求y關于x的函數解析式并求最大利潤．發布：2025/5/25 5:0:4組卷：140引用：6難度：0.5 -
3．某公司生產甲、乙兩種產品，已知生產甲種產品每千克的成本費是30元，生產乙種產品每千克的成本費是20元，物價部門規定，這兩種產品的銷售單價（每千克的售價）之和為80元，經市場調研發現，甲種產品的銷售單價為x（元），在公司規定30≤x≤60的范圍內，甲種產品的月銷售量y1（千克）符合y1=-2x+150，乙種產品的月銷售量y2（千克）與它的銷售單價成正比例，當乙產品單價為30元（即：80-x=30）時，它的月銷售量是30千克．
（1）求y2與x之間的函數關系式；
（2）公司怎樣定價，可使月銷售利潤最大？最大月銷售利潤是多少？（銷售利潤=銷售額-生產成本費）
（3）是否月銷售額越大月銷售利潤也越大？請說明理由．發布：2025/5/25 7:0:2組卷：1092引用：5難度：0.3