 操作計算:用尺規作圖法作正多邊形是數學史上很經典的幾何問題,在邊數小于10的正多邊形中,可以用尺規作圖法作出的有正三、正四、正五、正六和正八邊形,德國數學家高斯已經證明不能用尺規作圖法作出正七邊形和正九邊形,但是我們可以用下列方法近似地作出一個正七邊形:
操作計算:用尺規作圖法作正多邊形是數學史上很經典的幾何問題,在邊數小于10的正多邊形中,可以用尺規作圖法作出的有正三、正四、正五、正六和正八邊形,德國數學家高斯已經證明不能用尺規作圖法作出正七邊形和正九邊形,但是我們可以用下列方法近似地作出一個正七邊形:
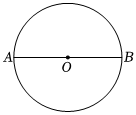
如圖,已知AB為⊙O的直徑.
步驟一:作出半徑OB的垂直平分線,與⊙O分別交于E,F兩點,垂足為D.
步驟二:以ED為半徑,在⊙O上依次截取BG=GH=HM=MN=NP=PQ=ED.
步驟三:順次連接各分點,即可得到一個近似的正七邊形BGHMNPQ.
(1)動手操作:請用上面方法,用直尺(沒有刻度)和圓規在已知⊙O中作出正七邊形BGHMNPQ.要求:不寫作法,但保留作圖痕跡.
(2)推理計算:若⊙O的半徑為1,則?EF的長度為 2π32π3,所作出的正七邊形BGHMNPQ的周長為 732732.
?
EF
2
π
3
2
π
3
7
3
2
7
3
2
【答案】;
2
π
3
7
3
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/21 18:30:1組卷:51引用:1難度:0.4
相似題
-
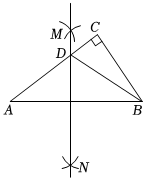 1.如圖,在Rt△ABC中,∠C=90°,按以下步驟作圖;①分別以點A,B為圓心,以大于AB的長為半徑作弧,兩弧相交于M,N兩點;②作直線MN,交AC于點D;③連接BD,若AD=13,CD=5,則BC的長為 .12發布:2025/5/22 5:0:1組卷:222引用:4難度:0.7
1.如圖,在Rt△ABC中,∠C=90°,按以下步驟作圖;①分別以點A,B為圓心,以大于AB的長為半徑作弧,兩弧相交于M,N兩點;②作直線MN,交AC于點D;③連接BD,若AD=13,CD=5,則BC的長為 .12發布:2025/5/22 5:0:1組卷:222引用:4難度:0.7 -
2.如圖1和圖2,已知點P是⊙O上一點,用直尺和圓規過點P作一條直線,使它與⊙O相切于點P.以下是甲、乙兩人的作法:
甲:如圖1,連接OP,以點P為圓心,OP長為半徑畫弧交⊙O于點A,連接并延長OA,再在OA上截取AB=OP,直線PB即為所求;
乙:如圖2,作直徑PA,在⊙O上取一點B(異于點P,A),連接AB和BP,過點P作∠BPC=∠A,則直線PC即為所求.
對于甲、乙兩人的作法,下列判斷正確的是( )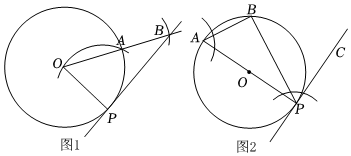
A.甲、乙兩人的作法都正確 B.甲、乙兩人的作法都錯誤 C.甲的作法正確,乙的作法錯誤 D.甲的作法錯誤,乙的作法正確 發布:2025/5/22 4:0:7組卷:625引用:14難度:0.5 -
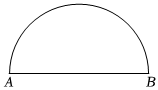 3.如圖,已知AB為半圓的直徑.求作矩形MNPQ,使得點M,N在AB上,點P,Q在半圓上,且MN=2MQ.
3.如圖,已知AB為半圓的直徑.求作矩形MNPQ,使得點M,N在AB上,點P,Q在半圓上,且MN=2MQ.
要求:(1)用直尺和圓規作圖;
(2)保留作圖的痕跡,寫出必要的文字說明.發布:2025/5/22 4:30:1組卷:649引用:1難度:0.7
相關試卷


