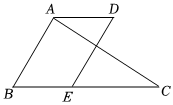
如圖，已知AB∥DE，∠BAC=90°．
（1）求證：AC⊥DE；
（2）若∠C+∠D=90°，求證：AD∥BC．

【答案】（1）證明見解答過程；
（2）證明見解答過程．

【解答】

【點評】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2025/6/6 16:0:1組卷：1099引用：3難度：0.7

相似題

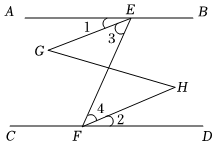1．完善證明過程：請在橫線上填寫結(jié)論并在括號中注明理由．
已知：如圖，直線EF分別交AB，CD于點E，F(xiàn)，∠1=∠2，∠G=∠H．
求證：∠BEF+∠EFD=180°．
證明：
∵∠G=∠H（已知）
∴GE∥
（
）
∴
=∠4（
）
又∵∠1=∠2（已知）
∴∠1+∠3=∠2+∠4
即∠AEF=
．
∴
∥CD（
）
∴∠BEF+∠EFD=180°（
）
發(fā)布：2025/6/7 5:30:3組卷：89引用：3難度：0.7
解析
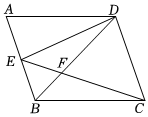2．如圖，AB∥CD，∠A=∠BCD，點E是AB上任意一點（不與A，B重合）．下列結(jié)論：①AD∥BC，②∠ADB=∠CDB，③∠DEC=∠ADE+∠BCE，④∠ABC=∠AED+∠ADE，⑤ED⊥CD．正確的有
．
發(fā)布：2025/6/7 5:30:3組卷：103引用：1難度：0.7
解析
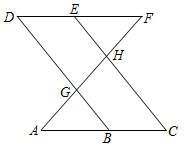3．如圖，點B、E分別在AC和DF上，若∠AGB=∠EHF，∠C=∠D，可以證明∠A=∠F．請完成下面證明過程中的各項“填空”．
證明：∵∠AGB=∠EHF（
），
∠AGB=
（對頂角相等），
∴∠EHF=∠DGF，
∴DB∥EC（
），
∴∠
=∠DBA（兩直線平行，同位角相等），
又∵∠C=∠D，
∴∠DBA=∠D，
∴DF∥
（內(nèi)錯角相等，兩直線平行），
∴∠A=∠F（
）．
發(fā)布：2025/6/7 5:30:3組卷：41引用：4難度：0.7
解析

相關(guān)試卷

如圖，已知AB∥DE，∠BAC=90°．（1）求證：AC⊥DE；（2）若∠C+∠D=90°，求證：AD∥BC．