【問題情境】
已知△ABC,AB=AC,點(diǎn)D,點(diǎn)E分別為BC,AC上的點(diǎn),且AD=AE,試探究∠BAD和∠CDE之間的關(guān)系.
對于這個(gè)問題,小明是這樣想的:
因?yàn)椤螧AD是△ABD的一個(gè)內(nèi)角,可得∠BAD+∠B+∠ADB=180°;因?yàn)椤螩DE是平角∠BDC的一部分,可得∠CDE+∠ADE+∠ADB=180°.對比這兩個(gè)等式發(fā)現(xiàn):∠BAD+∠B=∠CDE+∠ADE.那么∠BAD和∠CDE之間的關(guān)系與∠B和∠ADE的大小是否有關(guān)呢?
小明利用數(shù)學(xué)課上學(xué)習(xí)的“從特殊到一般”的思路,設(shè)計(jì)探究過程如下:
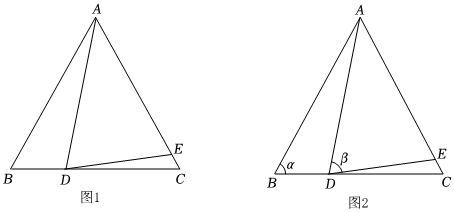
【從“特殊”入手】通過將∠B和∠ADE分別取特殊值,計(jì)算∠BAD和∠CDE的度數(shù)進(jìn)而判斷它們之間的關(guān)系.如下表:
| ∠B=50°,∠ADE=60° | ∠B=50°,∠ADE=70° | ∠B=40°,∠ADE=70° | |
| ∠BAD的度數(shù) |
20° 20°
|
40° 40°
|
60° 60°
|
| ∠CDE的度數(shù) |
10° 10°
|
20° 20°
|
30° 30°
|
∠CDE=∠BAD
1
2
∠CDE=∠BAD
.1
2
【探究“一般”規(guī)律】通過取特殊值探究.小明發(fā)現(xiàn)∠BAD和∠CDE之間的關(guān)系與∠B和∠ADE的大小無關(guān),于是設(shè)∠B=α,∠ADE=β,通過推理進(jìn)一步驗(yàn)證∠BAD和∠CDE之間的關(guān)系.請寫出推理過程.
【考點(diǎn)】三角形綜合題.
【答案】20°;40°;60°;10°;20°;30°;∠CDE=∠BAD
1
2
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:46引用:1難度:0.5
相似題
-
1.在△ABC中,CA=CB,∠ACB=α,點(diǎn)P是平面內(nèi)不與A,C重合的任意一點(diǎn),連接AP,將線段AP繞點(diǎn)P逆時(shí)針旋轉(zhuǎn)α得到線段DP,連接AD,BD,CP.
(1)觀察猜想
如圖1,當(dāng)α=60°時(shí),的值是 ,直線BD與直線CP相交所成的較小角的度數(shù)是 .BDCP
(2)類比探究
如圖2,當(dāng)α=90°時(shí),請寫出的值及直線BD與直線CP相交所成的小角的度數(shù),并就圖2的情形說明理由.BDCP
(3)解決問題
當(dāng)α=90°時(shí),若點(diǎn)E,F(xiàn)分別是CA,CB的中點(diǎn),點(diǎn)P在直線EF上,請直接寫出點(diǎn)C,P,D在同一直線上時(shí)的值.ADCP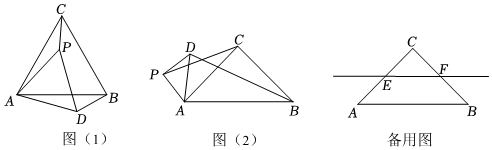 發(fā)布:2025/6/3 19:30:1組卷:540引用:4難度:0.3
發(fā)布:2025/6/3 19:30:1組卷:540引用:4難度:0.3 -
2.在平面直角坐標(biāo)系中,點(diǎn)A的坐標(biāo)為(8,0),點(diǎn)B為y軸正半軸上的一個(gè)動(dòng)點(diǎn),以B為直角頂點(diǎn),AB為直角邊在第一象限作等腰Rt△ABC.
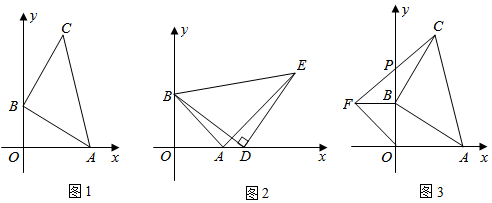
(1)如圖1,若OB=6,則點(diǎn)C的坐標(biāo)為 ;
(2)如圖2,若OB=8,點(diǎn)D為OA延長線上一點(diǎn),以D為直角頂點(diǎn),BD為直角邊在第一象限作等腰Rt△BDE,連接AE,求證:AE⊥AB;
(3)如圖3,以B為直角頂點(diǎn),OB為直角邊在第三象限作等腰Rt△OBF,連接CF,交y軸于點(diǎn)P,求線段BP的長.發(fā)布:2025/6/3 20:0:2組卷:987引用:6難度:0.2 -
3.閱讀以下材料,完成以下兩個(gè)問題.
[閱讀材料]已知:如圖,△ABC(AB≠AC)中,D、E在BC上,且DE=EC,過D作DF∥BA交AE于點(diǎn)F,DF=AC.求證:AE平分∠BAC.
結(jié)合此題,DE=EC,點(diǎn)E是DC的中點(diǎn),考慮倍長,并且要考慮連接哪兩點(diǎn),目的是證明全等,從而轉(zhuǎn)移邊和角.有兩種考慮方法:①考慮倍長FE,如圖(1)所示;②考慮倍長AE,如圖(2)所示
以圖(1)為例,證明過程如下:
證明:延長FE至G,使EG=EF,連接CG.
在△DEF和△CEG中,,ED=EC∠DEF=∠CEGEF=EG
∴△DEF≌△CEG(SAS).
∴DF=CG,∠DFE=∠G.
∵DF=AC,
∴CG=AC.
∴∠G=∠CAE.
∴∠DFE=∠CAE.
∵DF∥AB,
∴∠DFE=∠BAE.
∴∠BAE=∠CAE.
∴AE平分∠BAC.
問題1:參考上述方法,請完成圖(2)的證明.
問題2:根據(jù)上述材料,完成下列問題:
已知,如圖3,在△ABC中,AD是BC邊上的中線,分別以AB,AC為直角邊向外作等腰直角三角形,∠BAE=∠CAF=90°,AE=AB,AC=AF,AD=3,求EF的長.發(fā)布:2025/6/3 20:30:2組卷:2541引用:4難度:0.3


