（1）問題發現：如圖①，直線AB∥CD，E是AB與CD之間的一點，連接BE，CE，可以發現∠B+∠C=∠BEC．
請把下面的證明過程補充完整：
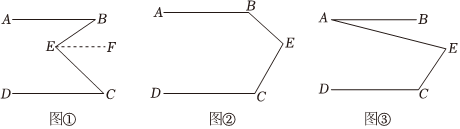
證明：過點E作EF∥AB，
∵AB∥CD（已知），EF∥AB（已作），
∴EF∥CD（ 平行于同一條直線的兩直線平行平行于同一條直線的兩直線平行）．
∴∠C=∠CEF（ 兩直線平行，內錯角相等兩直線平行，內錯角相等）．
∵EF∥AB，
∴∠B=∠BEF∠BEF（ 兩直線平行，內錯角相等兩直線平行，內錯角相等），
∵∠CEF+∠BEF=∠BEC，
∴∠B+∠C=∠BEC（等量代換）．
（2）拓展探究：如果點E運動到圖②所示的位置，其他條件不變，進一步探究發現：∠B，∠C，∠BEC之間的關系是 ∠B+∠C+∠BEC=360°∠B+∠C+∠BEC=360°；
（3）解決問題：如圖③，AB∥DC，∠C=120°，∠AEC=80°，請求出∠A的度數．
【考點】平行線的判定與性質．
【答案】平行于同一條直線的兩直線平行；兩直線平行，內錯角相等；∠BEF；兩直線平行，內錯角相等；∠B+∠C+∠BEC=360°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/25 8:0:9組卷：72引用：2難度：0.5
相似題
-
1．如圖，A、B、C三點在同一直線上，∠1=∠2．∠3=∠D、試說明BD∥CE．
證明：∵∠1=∠2（已知），
∴∥（ ）．
∴∠D=∠（ ）．
又∵∠D=∠3（ ），
∴∠=∠（ ）．
∴BD∥CE（ ）．發布：2025/5/30 17:30:1組卷：149引用：3難度：0.7 -
2．推理填空：已知，如圖，B、C、E共線，A、F、E共線，AB∥CD，∠1=∠2，∠3=∠4．
求證：AD∥BE．
證明：∵AB∥CD（已知），
∴∠4=∠（ ）．
∵∠3=∠4（已知），
∴∠3=∠（ ）．
∵∠1=∠2（已知），
∴∠1+∠CAF=∠2+∠CAF （ ）．
即∠BAF=∠DAC．
∴∠3=∠（ ）．
∴AD∥BE （ ）．發布：2025/5/30 20:0:1組卷：192引用：4難度：0.6 -
3．請閱讀小明同學在學習平行線這章知識點時的一段筆記，然后解決問題．
小明：老師說在解決有關平行線的問題時，如果無法直接得到角的關系，就需要借助輔助線來幫助解答，今天老師介紹了一個“美味”的模型---“豬蹄模型”．即
已知：如圖1，AB∥CD，E為AB、CD之間一點，連接AE，CE得到∠AEC．
求證：∠AEC=∠A+∠C．
小明筆記上寫出的證明過程如下：
證明：過點E作EF∥AB，
∴∠1=∠A．
∵AB∥CD，EF∥AB，
∴EF∥CD．
∴∠2=∠C．
∵∠AEC=∠1+∠2，
∴∠AEC=∠A+∠C．
請你利用“豬蹄模型”得到的結論或解題方法，完成下面的兩個問題．
（1）如圖2，若AB∥CD，∠E=60°，則∠B+∠C+∠F=．
（2）如圖3，AB∥CD，BE平分∠ABG，CF平分∠DCG，∠G=∠H+27°，E、B、H共線，F、C、H共線，則∠H=．
發布：2025/5/30 22:0:2組卷：2194引用：4難度：0.5