求代數(shù)式x2-4x+3的最小值時,我們通常運(yùn)用“a2≥0”.這個公式對代數(shù)式進(jìn)行配方來解決.比如x2-4x+3=x2-4x+4-1=(x-2)2-1,∵(x-2)2≥0,∴(x-2)2-1≥-1,∴x2-4x+3的最小值是-1,試?yán)谩芭浞椒ā苯鉀Q下列問題:
(1)填空:x2+6x+13=(x+33)2+44;
(2)求x2+y2+2x-4y+10的最小值;
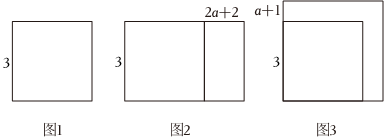
(3)如圖,將邊長為3的正方形一邊保持不變,另一組對邊增加2a+2(a>0)得到如圖2所示的新長方形,此長方形的面積為S1將正方形的邊長增加a+1(a>0),得到如圖3所示的新正方形,此正方形的面積為S2.
①用含a的代數(shù)式表示出S1,S2;
②比較S1,S2的大小.
【考點(diǎn)】配方法的應(yīng)用;非負(fù)數(shù)的性質(zhì):偶次方.
【答案】3;4
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/9/8 13:0:8組卷:79引用:1難度:0.5
相似題
-
1.“配方法”是指將一個式子或一個式子的某一部分通過恒等變形化為完全平方式或幾個完全平方式的和.它是數(shù)學(xué)的重要方法,可以解決多項式、方程的相關(guān)問題.如:我們可以通過“配方法”求代數(shù)式x2+4x+2的最小值.
x2-4x+2=x2-2?x?2+22-4+2=(x-2)2-2,
∵(x-2)2≥0,
∴當(dāng)x=2時,x2+4x+1有最小值-2.
請閱讀上述“配方法”的應(yīng)用,并解答下列問題:
(1)若x2+2x+5=(x+a)2+b,請求出a、b的值;
(2)試說明代數(shù)式6x-7-x2的值都不大于2;
(3)若代數(shù)式6x2+3kx+3的最小值為-3,試求出k的值.發(fā)布:2025/5/30 16:30:1組卷:98引用:1難度:0.7 -
2.請閱讀下列材料:
我們可以通過以下方法,求代數(shù)式x2+2x-3的最小值.
x2+2x-3=x2+2x+12-12-3=(x+1)2-4,
∵(x+1)2≥0,∴當(dāng)x=-1時,x2+2x-3有最小值-4.
請根據(jù)上述方法,解答下列問題:
(1)x2+6x+10=x2+2×3x+32-32+10=(x+a)2+b,則a=,b=;
(2)求證:無論x取何值,代數(shù)式x2+2x+5的值都是正數(shù);3
(3)若代數(shù)式x2-2kx+7的最小值為3,求k的值.發(fā)布:2025/5/30 14:30:1組卷:197引用:1難度:0.6 -
3.老師在講完乘法公式(a±b)2=a2±2ab+b2的各種運(yùn)用后,要求同學(xué)們運(yùn)用所學(xué)知識解答:求代數(shù)式x2+4x+5最小值?同學(xué)們經(jīng)過交流、討論,最后總結(jié)出如下解答方法:
解:x2+4x+5=(x+2)2+1
∵(x+2)2≥0∴(x+2)2+1≥1
即:當(dāng)(x+2)2=0時,x2+4x+5=(x+2)2+1的值最小,最小值是1,
請你根據(jù)上述方法,解答下列各題:
(1)直接寫出:(x+1)2-2的最小值為 ;
(2)求出代數(shù)式x2+10x+28的最小值;
(3)若x2+7x+y+2=0,求x+y的最大值.發(fā)布:2025/5/30 17:30:1組卷:508引用:2難度:0.5


