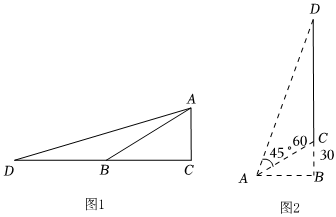
某數(shù)學(xué)興趣小組在探究如何求tan15°的值，經(jīng)過(guò)思考、討論、交流，得到以下思路：思路一：如圖1，在Rt△ABC中，∠C=90°，∠ABC=30°，延長(zhǎng)CB至點(diǎn)D，使BD=BA，連接AD．設(shè)AC=1，則BD=BA=2，BC=3．tanD=tan15°=12+3=2-3（2+3）（2-3）=2-3．思路二：利用科普書(shū)上的和（差）角正切公式：tan（α±β）=tanα±tanβ1+tanαtanβ．假設(shè)α=60°，β=45°代入差角正切公式：tan15°=tan（60°-45°）=tan60°-tan45°1+tan60°tan45°=3-11+3=2-3．請(qǐng)解決下列問(wèn)題（上述思路僅供參考）．
（1）類比：求出tan75°的值；
（2）應(yīng)用：如圖2，某電視塔建在一座小山上，山高BC為30米，在地平面上有一點(diǎn)A，測(cè)得A，C兩點(diǎn)間距離為60米，從A測(cè)得電視塔的視角（∠CAD）為45°，求這座電視塔CD的高度．
3
1
2
+
3
2
-
3
（
2
+
3
）
（
2
-
3
）
3
tanα
±
tanβ
1
+
tanαtanβ
tan
60
°
-
tan
45
°
1
+
tan
60
°
tan
45
°
3
-
1
1
+
3
3
【答案】（1）2+；
（2）（60+60）m．
3
（2）（60
3
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/25 13:0:1組卷：142引用：2難度：0.4
相似題
-
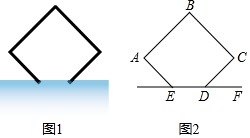1．如圖1是公園某處的幾何造型，如圖2是它的示意圖，正方形的一部分在水平面EF下方，測(cè)得DE=2米，∠CDF=45°，露出水平面部分的材料長(zhǎng)共合計(jì)140米（注：共8個(gè)大小一樣的正方形造型，不計(jì)損耗），點(diǎn)B到水平面EF的距離為 米．發(fā)布：2025/5/26 1:0:1組卷：124引用：2難度：0.4 -
2．我國(guó)紙傘的制作工藝十分巧妙．如圖1，傘不管是張開(kāi)還是收攏，傘柄AP始終平分同一平面內(nèi)兩條傘骨所成的角∠BAC，且AB=AC，從而保證傘圈D能沿著傘柄滑動(dòng)．如圖2是傘完全收攏時(shí)傘骨的示意圖，此時(shí)傘圈D已滑動(dòng)到點(diǎn)D'的位置，且A，B，D′三點(diǎn)共線，AD′=40cm,B為AD′中點(diǎn)．當(dāng)∠BAC=140°時(shí)，傘完全張開(kāi)．
（1）求AB的長(zhǎng)．
（2）當(dāng)傘從完全張開(kāi)到完全收攏，求傘圈D沿著傘柄向下滑動(dòng)的距離．
（參考數(shù)據(jù)：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）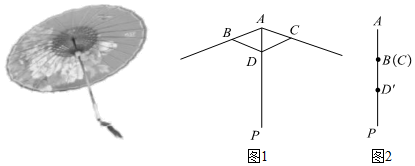
發(fā)布：2025/5/25 23:30:1組卷：2237引用：12難度：0.5 -
3．火災(zāi)是生活中最常見(jiàn)、最突出的一種災(zāi)難，消防車(chē)是救援火災(zāi)的主要裝備．圖1是一輛登高云梯消防車(chē)的實(shí)物圖，圖2是其工作示意圖，起重臂AC（10m≤AC≤20m）是可伸縮的，且起重臂AC可繞點(diǎn)A在一定范圍內(nèi)上下轉(zhuǎn)動(dòng)，張角∠CAE（90°≤∠CAE≤150°），轉(zhuǎn)動(dòng)點(diǎn)A距離地面的高度AE=3.5m.
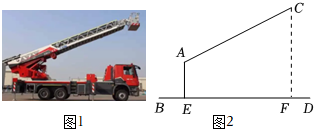
（1）當(dāng)起重臂AC的長(zhǎng)度為12m,張角∠CAE=120°，求云梯消防車(chē)最高點(diǎn)C距離地面的高度CF．
（2）某日一居民家突發(fā)火災(zāi)，該居民家距離地面的高度為180m,該消防車(chē)能否實(shí)施有效救援？（參考數(shù)據(jù)：≈1.732）3發(fā)布：2025/5/26 1:0:1組卷：172引用：1難度：0.5
相關(guān)試卷