閱讀下列材料，并回答問題．
[材料]自從《義務教育數學課程標準（2022年版）》實施以來，九年級的龍老師增加了一個習慣，就是在每個新章節備課時都會查閱新課標，了解該章知識的新舊課標的變化，并在上課時告訴學生．他通過查閱新課標獲悉：切線長定理由“選學”改為“必學”，并新增“會過圓外的一個點作圓的切線”．在學習完《切線的性質與判定》后，龍老師布置了一道課外思考題：“已知：如圖，⊙O及⊙O外一點P．求作：直線PM，使PM與⊙O相切于點M”．
班上小巖同學所在的學習小組經過探索，給出了如下的一種作圖方法：
（1）連接OP，以O為圓心，OP長為半徑作大圓O；
（2）若OP交小圓O于點N，過點N作小圓O的切線與大圓O交于A，B兩點（點A在點B的上方）；
（3）連接AO交小圓O于M，連接PM，則PM是小圓O的切線．
[問題]
（1）請問小巖同學所在的學習小組提供的作圖方法是否正確？請你按照步驟完成作圖（尺規作圖，保留作圖痕跡），并說明理由．
（2）延長AO交大圓O于C，連接CN，若OA=2，OM=1，求CN的長．
【考點】圓的綜合題．
【答案】（1）小巖同學所在的學習小組提供的作圖方法正確．理由見解析；（2）．
7
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/30 11:30:2組卷：260引用：1難度：0.4
相似題
-
1．如圖1，C、D是以AB為直徑的⊙O上的點，且滿足BC=CD=DA=3，點P在
上，PD交AC于點M，交AB于點G，PC交BD于點N，交AB于點H．?AB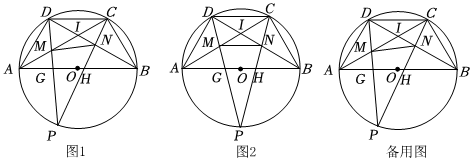
（1）求∠DBA的度數．
（2）如圖2，當點P是的中點時，?AB
①求證：△AMG是等腰三角形．
②求的值．MIAG
（3）如圖1，設，△DMI與△CNI的面積差為y,求y關于x的函數表達式．AMMC=x發布：2025/5/31 16:30:2組卷：434引用：1難度：0.2 -
2．閱讀材料：如圖，△ABC的周長為l,面積為S，內切圓⊙O的半徑為r,探究r與S，l之間的關系．
解：連接OA、OB、OC．
∵S△AOB=AB?r,S△OBC=12BC?r,S△OCA=12CA?r,12
∴S=AB?r+12BC?r+12CA?r=12l?r,12
∴r=2Sl
解決問題：
（1）利用探究的結論，計算邊長分別為5，12，13的三角形內切圓半徑．
（2）如圖，若四邊形ABCD存在內切圓（與各邊都相切的圓），且面積為S，各邊長分別為a,b,c,d,試推導四邊形的內切圓半徑公式．
（3）若一個n邊形（n為不小于3的整數）存在內切圓，且面積為S，各邊長分別為a1，a2，a3，a4，…，an，合理猜想其內切圓半徑公式（不需說明理由）．發布：2025/5/31 13:0:2組卷：90引用：2難度：0.5 -
3．如圖，平面直角坐標系中，矩形ABCD，其中A（1，0）、B（4，0）、C（4，2）、D（1，2），定義如下：若點P關于直線l的對稱點P'在矩形ABCD的邊上，則稱點P為矩形ABCD關于直線l的“關聯點”，
（1）已知點P1（-1，2）、點P2（-2，1）、點P3（-4，1），點P2（-3，-1）中是矩形ABCD關于y軸的關聯點的是 ；
（2）⊙O的圓心O（-，1）半徑為72，若⊙O上至少存在一個點是矩形ABCD關于直線x=t的關聯點，求t的取值范圍；32
（3）⊙O的圓心O（m,1）（m＜0）半徑為r,若存在t值使⊙O上恰好存在四個點是矩形ABCD關于直線x=t的關聯點，寫出r的取值范圍，并寫出當r取最小值時t的取值范圍（用含m的式子表示）．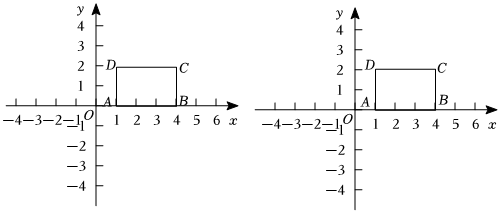
發布：2025/5/31 11:0:1組卷：360引用：1難度：0.2