如圖,海事救援指揮中心A接到海上SOS呼救:一艘漁船B在海上碰到暗礁,船體漏水下沉,5名船員需要援救.經測量漁船B到海岸最近的點C的距離BC=20km,∠BAC=22°37′,指揮中心立即制定三種救援方案(如圖1):
①派一艘沖鋒舟直接從A開往B;②先用汽車將沖鋒舟沿海岸線送到點C,然后再派沖鋒舟前往B;③先用汽車將沖鋒舟沿海岸線送到距指揮中心33km的點D,然后再派沖鋒舟前往B.
已知沖鋒舟在海上航行的速度為60km/h,汽車在海岸線上行駛的速度為90km/h.
(sin22°37′=513,cos22°37′=1213,tan22°37′=512)
(1)通過計算比較,這三種方案中,哪種方案較好(汽車裝卸沖鋒舟的時間忽略不計)?
(2)事后,細心的小明發現,上面的三種方案都不是最佳方案,最佳方案應是:先用汽車將沖鋒舟沿海岸線送到點P處,點P滿足cos∠BPC=23(沖鋒舟與汽車速度的比),然后再派沖鋒舟前往B(如圖2).請你說明理由!
如果你反復探索沒有解決問題,可以選取①、②、③兩種研究方法:
方案①:在線段上AP任取一點M;然后用轉化的思想,從幾何的角度說明汽車行AM加上沖鋒舟行BM的時間比車行AP加上沖鋒舟行BP的時間要長.
方案②:在線段上AP任取一點M;設AM=x;然后用含有x的代數式表示出所用時間t;
方案③:利用現有數據,根據cos∠BPC=23計算出汽車行AP加上沖鋒舟行BP的時間.

5
13
12
13
5
12
2
3
2
3
【考點】解直角三角形的應用-方向角問題.
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:400引用:4難度:0.5
相似題
-
 1.湘江流經永州、衡陽、株洲、湘潭、長沙等市,至岳陽注入洞庭湖,干流全長844公里,是湖南省內最大的河流,在一次數學活動課上,老師帶領學生去測量湘江某段的寬度(假設兩岸是平行的),如圖,某學生在河東岸點A處觀測河對岸水邊點C,測得C在A北偏西30°的方向上,沿河岸向北前行400米到達B處,測得C在B北偏西60°的方向上.
1.湘江流經永州、衡陽、株洲、湘潭、長沙等市,至岳陽注入洞庭湖,干流全長844公里,是湖南省內最大的河流,在一次數學活動課上,老師帶領學生去測量湘江某段的寬度(假設兩岸是平行的),如圖,某學生在河東岸點A處觀測河對岸水邊點C,測得C在A北偏西30°的方向上,沿河岸向北前行400米到達B處,測得C在B北偏西60°的方向上.
(1)求BC的長;
(2)求此段湘江的寬度.(結果精確到0.1,參考數據:≈1.414,2≈1.732).3發布:2025/5/26 8:0:5組卷:384引用:3難度:0.5 -
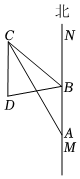 2.如圖,梁子湖區天空之境景區為了方便游客行走準備修建一條南北走向的棧道CD,景區道路MN與CD平行.在景區道路MN上的點A處測得棧道的一端C位于北偏西30°方向,沿景區道路MN向正北方向行走6km到達點B,測得棧道的一端C位于北偏西45°方向,棧道的另一端D位于南偏西75°方向.
2.如圖,梁子湖區天空之境景區為了方便游客行走準備修建一條南北走向的棧道CD,景區道路MN與CD平行.在景區道路MN上的點A處測得棧道的一端C位于北偏西30°方向,沿景區道路MN向正北方向行走6km到達點B,測得棧道的一端C位于北偏西45°方向,棧道的另一端D位于南偏西75°方向.
(1)求點B到點C的距離;
(2)求棧道CD的長度.發布:2025/5/26 8:30:1組卷:90引用:1難度:0.5 -
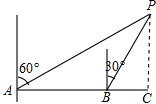 3.如圖,一艘輪船在A處測得燈塔P位于其北偏東60°方向上,輪船沿正東方向航行30海里到達B處后,此時測得燈塔P位于其北偏東30°方向上,此時輪船與燈塔P的距離是( )
3.如圖,一艘輪船在A處測得燈塔P位于其北偏東60°方向上,輪船沿正東方向航行30海里到達B處后,此時測得燈塔P位于其北偏東30°方向上,此時輪船與燈塔P的距離是( )A.15 海里3B.30海里 C.45海里 D.30 海里3發布:2025/5/26 9:0:1組卷:2352引用:11難度:0.7


