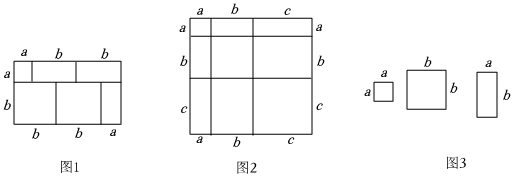
我們知道,對于同一個圖形,通過用不同的方法計算它的面積,可以得到一個數學等式,例如:由圖1可以得到(a+2b)(a+b)=a2+3ab+2b2.
(1)由圖2可以得到的數學等式是 (a+b+c)2=a2+b2+c2+2ab+2ac+2bc(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)利用(1)中所得到的結論,解決問題:已知a+b+c=9,ab+bc+ac=29,求a2+b2+c2的值;
(3)小明同學打算用圖3中的x張邊長為a的正方形紙片,y張邊長為b的正方形紙片,z張長為b、寬為a的長方形紙片,拼出一個面積為(3a+5b)(4a+7b)的長方形,那么他總共需要多少張紙片?
【答案】(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:28引用:1難度:0.5
相似題
-
1.對于一個三位自然數n,若將n的任意兩個數位的數對調后得到一個新三位數記為n'=100×a+10×b+c,其中a,b,c都是不小于1且不大于9的自然數,在所有的n'中,我們規定當|a-b-c|最小時的三位自然數n'是“n的好數”,并記S(n)=a-bc.例如由234得到的243,324,432中,因為|2-4-3|=5,|3-2-4|=3,|4-3-2|=1,1<3<5,所以432是“234的好數”,記S(234)=4-2×3=-2,則n'=432或423.
(1)求S(156);
(2)設三位自然數n的百位和十位的數分別是x,y,個位數是6,且3x+y=17,若n'是“n的好數”,當S(n)取最大值時,求n'.發布:2025/6/8 19:30:1組卷:156引用:2難度:0.7 -
2.如果一個四位數M滿足各個數位數字都不為0,且千位數字與百位數字之和為9,將M的千位數字與百位數字組成的兩位數記為x,十位數字與個位數字組成的兩位數記為y,令F(M)=
,若F(M)為整數,則稱數M是“久久為功數”.x+2y9
例如:M=2754,∵2+7=9,x=27,y=54,F(M)==15為整數,∴M=2754是“久久為功數”;又如:M=6339,∵6+3=9,x=63,y=39,F(M)=27+2×549=63+2×399不為整數,∴M=6339不是“久久為功數”.473
(1)判斷1827,4532是否是“久久為功數”,并說明理由;
(2)把一個“久久為功數”M的千位數字記為a,十位數字記為b,個位數字記為c,令G(M)=,當G(M)為整數時,求出所有滿足條件的M.2c-3a2b+3a發布:2025/6/8 21:0:2組卷:111引用:1難度:0.5 -
3.若把一個多位正整數的個位數字截去,再用余下的數加上截去的個位數字的4倍,如果和是13的倍數,則原數能被13整除.例如,判斷19669是否能被13整除的過程如下:1966+9×4=2002,200+2×4=208,20+8×4=52,52是13的倍數,所以19669能被13整除.能被13整除的數叫“十三數”.
(1)請用上述方法判斷2821和6736是否能被13整除,并說明理由;
(2)一個三位數是一個“十三數”,其中x,y,z均為非零整數,x<y<z,1≤x,y,z≤9,若M的十位數字是百位數字與個位數字的平均數,則稱M為“平衡數”,并記M=xyz,求F(M)的值.F(M)=|x-y|z+1發布:2025/6/8 20:30:2組卷:120引用:2難度:0.7


