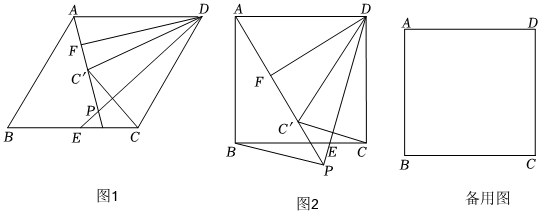
如圖1，菱形ABCD中，∠B=60°，AB=2，E是邊BC上一動點（不與點B，C重合），連結DE，點C關于直線DE的對稱點為C′，連結AC?并延長交直線DE于點P，F是AC′的中點，連結DC?，DF．
（1）填空：DC?=22；∠FDP=30°30°．
（2）如圖2，將題中條件“∠B=60°”改成“∠B=90°”，其余條件均不變，連結BP，猜想AP，BP，DP這三條線段間的數量關系，并對你的猜想加以證明．
（3）在（2）的條件下，連結AC．
①若動點E運動到邊BC的中點處時，求△ACC′的面積．
②在動點E的整個運動過程中，求△ACC′面積的最大值．
【考點】四邊形綜合題．
【答案】2；30°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/1 8:0:8組卷：123引用：2難度：0.4
相似題
-
1．在平面直角坐標系xOy中，對于點P（x1，y1），給出如下定義：當點Q（x2，y2）滿足x1?x2=y1?y2時，稱點Q是點P的等積點．已知點P（1，2）．
（1）在Q1（2，1），Q2（-4，-1），Q3（8，2）中，點P的等積點是 ．
（2）點Q是P點的等積點，點C在x軸上，以O，P，Q，C為頂點的四邊形是平行四邊形，求點C的坐標．
（3）已知點和點M（4，m），點N是以點M為中心，邊長為2且各邊與坐標軸平行的正方形T上的任意一點，對于線段BN上的每一點A，在線段PB上都存在一個點R使得A為R的等積點，直接寫出m的取值范圍．B（1，12）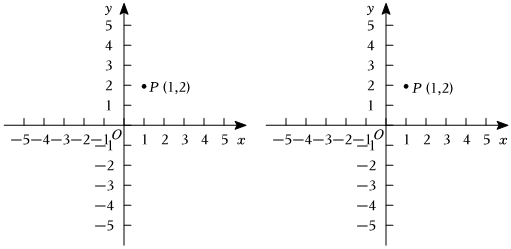
發布：2025/6/10 1:0:1組卷：129引用：1難度：0.9 -
2．如圖所示，四邊形ABCD為菱形，AD=5，sinB=，點E為邊AB上一動點（不與端點重合），△DEF與△DEA關于DE對稱．2425
（1）試求菱形ABCD的面積；
（2）若點D、B、F共線，求AE的長；
（3）點G為邊CD上一點，且CG=1，連接GF、BF，試求BF+2GF的最小值．發布：2025/6/10 3:30:1組卷：283引用：2難度：0.1 -
3．感知：數學課上，老師給出了一個模型：如圖1，點A在直線DE上，且∠BDA=∠BAC=∠AEC=90°，像這種一條直線上的三個頂點含有三個相等的角的模型我們把它稱為“一線三等角“模型．
應用：（1）如圖2，Rt△ABC中，∠ACB=90°，CB=CA，直線ED經過點C，過A作AD⊥ED于點D，過B作BE⊥ED于點E．求證：△BEC≌△CDA．
（2）如圖3，在△ABC中，D是BC上一點，∠CAD=90°，AC=AD，∠DBA=∠DAB，AB=2，求點C到AB邊的距離．3
（3）如圖4，在?ABCD中，E為邊BC上的一點，F為邊AB上的一點．若∠DEF=∠B，AB=10，BE=6，求的值．EFDE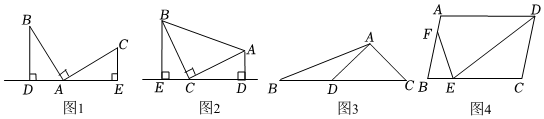
發布：2025/6/10 1:30:1組卷：2068引用：10難度：0.4