2023年浙江省紹興市上虞區中考數學適應性試卷

一、選擇題。(本大題有10小題，每小題4分，共40分。請選出每小題中一個最符合題意的選項、不選、多選、錯選，均不給分)

• 1．實數2，0，-2，

  2

  中，最小的實數是（　　）

  A．2

  B．0

  C．-2

  D． 2
  組卷：44引用：3難度：0.8

  解析

• 2．根據全國第七次人口普查結果表明，2022年紹興市常住人口總數約為5337000，數字5337000用科學記數法表示是（　　）

  A．5.337×107

  B．5.337×106

  C．0.5337×108

  D．53.37×105
  組卷：24引用：3難度：0.9

  解析

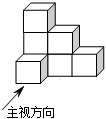• 3．由七個相同的小立方塊搭成的幾何體如圖所示，則它的主視圖是（　　）

  A．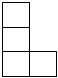

  B．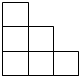

  C．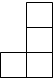

  D．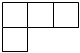
  組卷：366引用：7難度：0.9

  解析

• 4．在一個不透明的袋子里，裝有3個紅球，2個白球，1個黃球，它們除顏色外都相同，從袋中任意摸出一個球為白球的概率是（　　）

  A． 3 4

  B． 1 2

  C． 1 3

  D． 1 4
  組卷：125引用：5難度：0.8

  解析

• 5．下列計算正確的是（　　）

  A．（a2-ab）÷a=a-ab	B．3a2?a=3a3
  C．（a-b）2=a2-b2	D．（a2）3=a5
  組卷：128引用：4難度：0.7

  解析

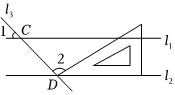• 6．如圖，直線l₁∥l₂，分別與直線l₃交于C，D兩點，把一塊含30°角的三角板按如圖所示的位置擺放，若∠1=45°，則∠2的度數為（　　）

  A．90°

  B．95°

  C．100°

  D．105°
  組卷：103引用：3難度：0.7

  解析

• 7．已知二次方程x²+bx+c=0的兩根為-1和5，則對于二次函數y=x²+bx+c,下列敘述正確的是（　　）

  A．當x=2時，函數的最大值是9

  B．當x=-2時，函數的最大值是9

  C．當x=2時，函數的最小值是-9

  D．當x=-2時，函數的最小值是-9
  組卷：233引用：2難度：0.7

  解析

• 8．如圖，菱形ABCD中，點O為對稱中心，點E從點A出發沿AB向點B移動，移動到點B停止，作射線EO，交邊CD于點F，則四邊形AECF形狀的變化依次為（　　）

  A．平行四邊形→正方形→平行四邊形→矩形

  B．平行四邊形→矩形→平行四邊形→菱形

  C．平行四邊形→正方形→菱形→矩形

  D．平行四邊形→菱形→正方形→矩形
  組卷：93引用：2難度：0.7

  解析

三、解答題。(本大題有8小題，第17~20小題每小題8分，第21小題10分,第22.23小題每小題8分，第24小題14分,共80分，解答需寫出必要的文字說明、演算步驟或證明過程)

• 23．在平面直角坐標系中，當x=-2和x=4時，二次函數y=ax²+bx-2（a,b是常數，a≠0）的函數值相等．
  （1）若該函數的最大值為1，求函數的表達式，并寫出函數圖象的頂點坐標．
  （2）若該函數的圖象與x軸有且只有一個交點，求a,b的值．
  （3）記（2）中的拋物線為y₁，將拋物線y₁向上平移2個單位得到拋物線y₂，當-2≤x≤m時，拋物線y₂的最大值與最小值之差為8，求m的值．
  組卷：588引用：3難度：0.4

  解析

• 24．如圖1，菱形ABCD中，∠B=60°，AB=2，E是邊BC上一動點（不與點B，C重合），連結DE，點C關于直線DE的對稱點為C′，連結AC?并延長交直線DE于點P，F是AC′的中點，連結DC?，DF．
  （1）填空：DC?=

  ；∠FDP=

  ．
  （2）如圖2，將題中條件“∠B=60°”改成“∠B=90°”，其余條件均不變，連結BP，猜想AP，BP，DP這三條線段間的數量關系，并對你的猜想加以證明．
  （3）在（2）的條件下，連結AC．
  ①若動點E運動到邊BC的中點處時，求△ACC′的面積．
  ②在動點E的整個運動過程中，求△ACC′面積的最大值．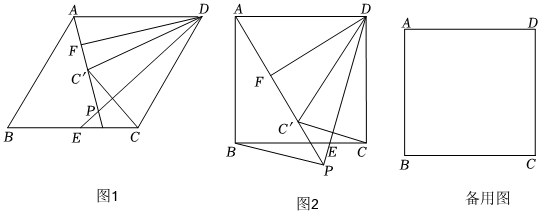
  
  組卷：123引用：2難度：0.4

  解析