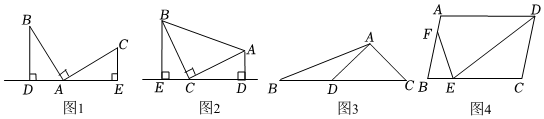
感知：數(shù)學課上，老師給出了一個模型：如圖1，點A在直線DE上，且∠BDA=∠BAC=∠AEC=90°，像這種一條直線上的三個頂點含有三個相等的角的模型我們把它稱為“一線三等角“模型．
應用：（1）如圖2，Rt△ABC中，∠ACB=90°，CB=CA，直線ED經(jīng)過點C，過A作AD⊥ED于點D，過B作BE⊥ED于點E．求證：△BEC≌△CDA．
（2）如圖3，在△ABC中，D是BC上一點，∠CAD=90°，AC=AD，∠DBA=∠DAB，AB=23，求點C到AB邊的距離．
（3）如圖4，在?ABCD中，E為邊BC上的一點，F(xiàn)為邊AB上的一點．若∠DEF=∠B，AB=10，BE=6，求EFDE的值．
3
EF
DE
【考點】四邊形綜合題．
【答案】（1）見解析；
（2）；
（3）．
（2）
3
（3）
3
5
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：2060引用：10難度：0.4
相似題
-
1．如圖1，四邊形ABCD為正方形，點E為其邊BC上一點，以CE為邊在正方形ABCD右側(cè)作正方形CEFG，將正方形CEFG繞點C逆時針旋轉(zhuǎn)，記旋轉(zhuǎn)角為α（0°＜α＜360°），連接AF、BG，直線AF、BG交于點M．
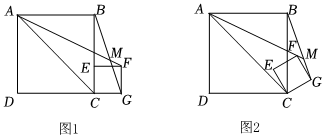
（1）當α=90°時，∠AMB=°；當α=270°時，∠AMB=°；
（2）在旋轉(zhuǎn)過程中，∠AMB的度數(shù)是否為定值？如果是，請就圖2的情況予以證明；如果不是，請說明理由．
（3）若BC=3，CE=1，當A、E、F三點在同一條直線上時，請直接寫出線段BM的長度．發(fā)布：2025/5/25 13:0:1組卷：152引用：1難度：0.1 -
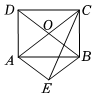2．如圖，矩形ABCD的對角線AC，BD相交于點O，△AOB關于AB的對稱圖形為△AEB．
（1）求證：四邊形AEBO是菱形；
（2）連接CE，若AB=6cm,CB=cm.21
①求sin∠ECB的值；
②若點P為線段CE上一動點（不與點C重合），連接OP，一動點Q從點O出發(fā)，以1cm/s的速度沿線段OP勻速運動到點P，再以2.5cm/s的速度沿線段PC勻速運動到點C，到達點C后停止運動，當點Q沿上述路線運動到點C所需要的時間最短時，求PC的長和點Q走完全程所需的時間．發(fā)布：2025/5/25 13:30:1組卷：46引用：2難度：0.3 -
3．課本再現(xiàn)
（1）在證明“三角形內(nèi)角和定理”時，小明只撕下三角形紙片的一個角拼成圖1即可證明，其中與∠A相等的角是 ；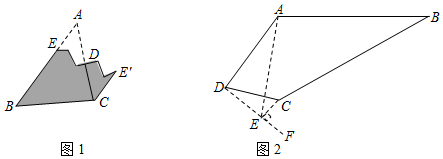
類比遷移
（2）如圖2，在四邊形ABCD中，∠ABC與∠ADC互余，小明發(fā)現(xiàn)四邊形ABCD中這對互余的角可類比（1）中思路進行拼合：先作∠CDF=∠ABC，再過點C作CE⊥DF于點E，連接AE，發(fā)現(xiàn)AD，DE，AE之間的數(shù)量關系是 ；
方法運用
（3）如圖3，在四邊形ABCD中，連接AC，∠BAC=90°，點O是△ACD兩邊垂直平分線的交點，連接OA，∠OAC=∠ABC．
①求證：∠ABC+∠ADC=90°；
②連接BD，如圖4，已知AD=m,DC=n,=2，求BD的長（用含m,n的式子表示）．ABAC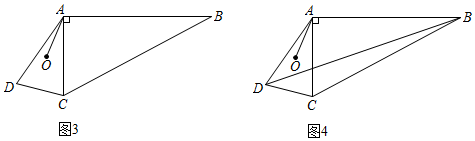
發(fā)布：2025/5/25 13:30:1組卷：2913引用：8難度：0.1