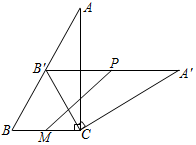
在Rt△ABC中，∠ACB=90°，將△ABC繞頂點C順時針旋轉得到△A′B′C′，點M是BC的中點，點P是A′B′的中點，連接PM．若BC=2，∠A=30°，線段PM長度的最大值是
3
3
．

【答案】3

【解答】

【點評】

聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。

發(fā)布：2025/6/3 18:0:1組卷：1008引用：2難度：0.5

相似題

1．如圖，把Rt△ABC繞頂點C順時針旋轉90°得到Rt△DFC，若直線DF垂直平分AB，垂足為點E，連接BF，CE，AD，且BC=2，CE=BE．下面四個結論：
①BF=
2
2
；②∠CBF=45°；③∠CED=30°；④△ECD的面積為
2
2
+4，
其中正確的結論有
．
發(fā)布：2025/6/5 12:0:1組卷：59引用：1難度：0.5
解析
2．如圖，△ABC為等邊三角形，點F是線段AC上一點（點F不與A，C重合），連接BF，過點A作AD⊥BF，垂足為點D，將線段AD繞點A順時針旋轉60°得到線段AE，連接DE，CE．
（1）如圖1，求證：AE⊥CE；
（2）如圖2，延長ED交BC于點M，求證：M為BC的中點．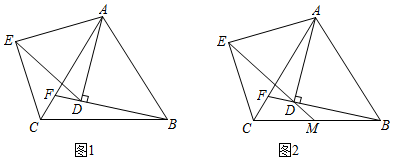
發(fā)布：2025/6/5 12:30:2組卷：205引用：4難度：0.7
解析
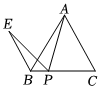3．如圖，P為等邊△ABC的邊BC上任一點，連接PA，將線段PA繞點P逆時針旋轉60°得線段PE，連接BE，則∠CBE的度數(shù)為
．
發(fā)布：2025/6/5 13:30:2組卷：34引用：1難度：0.5
解析

相關試卷

在Rt△ABC中，∠ACB=90°，將△ABC繞頂點C順時針旋轉得到△A′B′C′，點M是BC的中點，點P是A′B′的中點，連接PM．若BC=2，∠A=30°，線段PM長度的最大值是33．