在《九章算術》中有求三角形面積的公式“底乘高的一半”,但是在實際丈量土地面積時,準確測量高并不容易,所以古人想到了能否利用三角形的三條邊長來求面積.我國南宋著名的數學家秦九韶(約1202~約1261)提出了“三斜求積術”,簡稱秦九韶公式.古希臘的幾何學家海倫(Heron,約公元50年)在數學史上以解決幾何測量問題而聞名.在他的著作《度量》一書中,給出了利用三角形三邊長求面積的方法和證明,相傳這個公式最早是由古希臘數學家阿基米德(公元前287年—公元前212年)得出的.在我國稱這個公式為海倫—秦九韶公式.它的表述為:如果一個三角形三邊長分別為a、b、c,那么三角形的面積為S=p(p-a)(p-b)(p-c).(公式里的p為半周長,即p=a+b+c2)
請利用海倫——秦九韶公式解決以下問題:
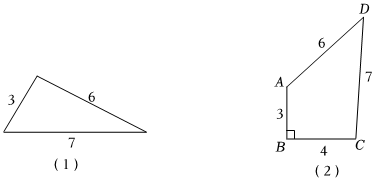
(1)三邊長分別為3、6、7的三角形面積為 4545.
(2)四邊形ABCD中,AB=3,BC=4,CD=7,AD=6,∠B=90°,求該四邊形的面積.
S
=
p
(
p
-
a
)
(
p
-
b
)
(
p
-
c
)
p
=
a
+
b
+
c
2
5
5
【考點】二次根式的應用.
【答案】4
5
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:169引用:2難度:0.6
相似題
-
1.小明在解方程
-24-x=2時采用了下面的方法:由8-x
(-24-x)(8-x+24-x)=(8-x)2-(24-x)2=(24-x)-(8-x)=16,8-x
又有-24-x=2,可得8-x+24-x=8,將這兩式相加可得8-x,將24-x=58-x=3=5兩邊平方可解得x=-1,經檢驗x=-1是原方程的解.24-x
請你學習小明的方法,解下面的方程:
(1)方程的解是 ;x2+42+x2+10=16
(2)解方程+4x2+6x-5=4x.4x2-2x-5發布:2025/5/31 20:0:2組卷:8326引用:11難度:0.1 -
2.某居民小區有塊形狀為矩形ABCD的綠地,長BC為
米,寬AB為128米,現在要矩形綠地中修建兩個形狀大小相同的長方形花壇(即圖中陰影部分),每個長方形花壇的長為50米,寬為(13+1)米.(13-1)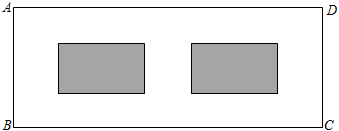
(1)求矩形ABCD的周長.(結果化為最簡二次根式)
(2)除去修建花壇的地方,其它地方全修建成通道,通道上要鋪上造價為6元/平方米的地磚,要鋪完整個通道,則購買地磚需要花費多少元?發布:2025/5/31 21:0:1組卷:447引用:6難度:0.6 -
3.已知長方形長a=
,寬b=1248.1327
①求長方形的周長;
②求與長方形等面積的正方形的周長,并比較長方形周長與正方形周長大小關系.發布:2025/5/31 17:30:1組卷:1217引用:10難度:0.5


