2021-2022學年河南省許昌市長葛市八年級（下）期中數學試卷

一、選擇題（本大題共10小題，每小題3分，共30分，每小題中均有四個結論供選擇，其中只有一個結論是正確的，請將你選擇的結果涂在答題卡對應位置）

• 1．下列根式中，不是最簡二次根式的是（　　）

  A． 0 . 5

  B． 3

  C． 7

  D． 2
  組卷：11引用：1難度：0.8

  解析

• 2．要使式子

  2

  x

  +

  3

  有意義，字母x的取值應滿足（　　）

  A． x ≥ - 2 3

  B． x ≤ - 2 3

  C． x ≥ - 3 2

  D． x ≤ 3 2
  組卷：45引用：1難度：0.7

  解析

• 3．下列各組線段中，能構成直角三角形的是（　　）

  A．2，3，4

  B．3，4，6

  C．5，12，13

  D．4，6，7
  組卷：1398引用：61難度：0.9

  解析

• 4．計算

  18

  -

  2

  的結果是（　　）

  A．4

  B．3

  C．2 2

  D． 2
  組卷：16引用：3難度：0.8

  解析

• 5．在Rt△ABC中，斜邊BC=

  2

  ，則AB²+AC²+BC²的值為（　　）

  A． 2

  B． 2 2

  C．2

  D．4
  組卷：57引用：2難度：0.8

  解析

• 6．下列命題中，正確的是（　　）

  A．對角線相等的四邊形是矩形

  B．對角線互相平分的四邊形是平行四邊形

  C．對角線互相垂直的四邊形是菱形

  D．對角線互相垂直且相等的四邊形是正方形
  組卷：389引用：31難度：0.9

  解析

• 7．若a,b為直角三角形的兩直角邊，c為斜邊，下列選項中不能用來證明勾股定理的是（　　）

  A．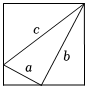

  B．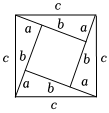

  C．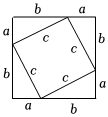

  D．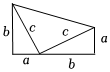
  組卷：377引用：4難度：0.6

  解析

三、解答題（共8小題，75分，請將解答結果填在答題卡上對應位置）

• 22．在8×6的正方形網格中，正方形網格的邊長為單位1；已知△ABC頂點均在格點上，請用無刻度直尺畫圖：
  （1）在圖1中，畫一個與△ABC面積相等，且以BC為邊的平行四邊形，頂點在格點上；
  （2）在圖2中，畫一個與△ABC面積相等，且以點C為其中一個頂點的正方形，頂點也在格點上．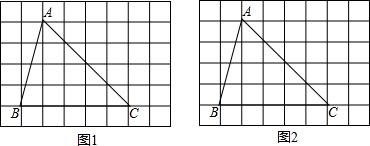
  
  組卷：141引用：3難度：0.5

  解析

• 23．在《九章算術》中有求三角形面積的公式“底乘高的一半”，但是在實際丈量土地面積時，準確測量高并不容易，所以古人想到了能否利用三角形的三條邊長來求面積．我國南宋著名的數學家秦九韶（約1202～約1261）提出了“三斜求積術”，簡稱秦九韶公式．古希臘的幾何學家海倫（Heron,約公元50年）在數學史上以解決幾何測量問題而聞名．在他的著作《度量》一書中，給出了利用三角形三邊長求面積的方法和證明，相傳這個公式最早是由古希臘數學家阿基米德（公元前287年—公元前212年）得出的．在我國稱這個公式為海倫—秦九韶公式．它的表述為：如果一個三角形三邊長分別為a、b、c,那么三角形的面積為

  S

  =

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  ．（公式里的p為半周長，即

  p

  =

  a

  +

  b

  +

  c

  2

  ）
  請利用海倫——秦九韶公式解決以下問題：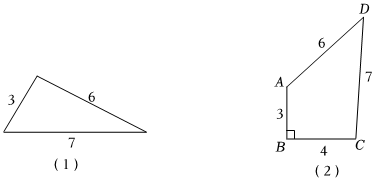
  
  （1）三邊長分別為3、6、7的三角形面積為

  ．
  （2）四邊形ABCD中，AB=3，BC=4，CD=7，AD=6，∠B=90°，求該四邊形的面積．
  組卷：169引用：2難度：0.6

  解析