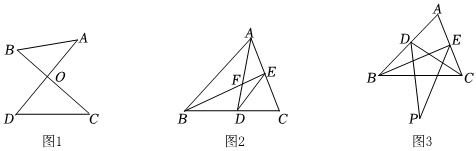
我們將內角互為對頂角的兩個三角形稱為“對頂三角形”．例如，在圖1中，△AOB的內角∠AOB與△COD的內角∠COD互為對頂角，則△AOB與∠COD為“對頂三角形”，根據三角形內角和定理知“對頂三角形”有如下性質：∠A+∠B=∠C+∠D．
性質理解：
（1）如圖1，在“對頂三角形”△AOB與∠COD中，則∠AOB=70°，則∠C+∠D=110110°．
性質應用：
（2）如圖2，在△ABC中，AD、BE分別平分∠BAC和∠ABC，若∠C=60°，∠ADE比∠BED大6°，求∠BED的度數．
拓展提高：
（3）如圖3，BE、CD是△ABC的角平分線，且∠BDC和∠BEC的平分線DP和EP相交于點P，設∠A=α，直接寫出∠P的度數（用含α的式子表示∠P）．
【考點】三角形內角和定理．
【答案】110
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 18:0:1組卷：936引用：2難度：0.5
相似題
-
1．如圖，AD是△ABC的高，AE平分∠BAC．
（1）若∠B=64°，∠C=48°，求∠DAE的度數；
（2）若∠B-∠C=32°，求∠DAE的度數．發布：2025/6/3 4:30:1組卷：511引用：4難度：0.5 -
2．如圖，AE平分∠BAC，∠CAE=∠CEA．
（1）AB與CD有怎樣的位置關系？為什么？
（2）若∠C=50°，求∠CEA的度數．發布：2025/6/3 6:30:2組卷：86引用：3難度：0.7 -
3．（問題背景）
∠MON=90°，點A、B分別在OM、ON上運動（不與點O重合）．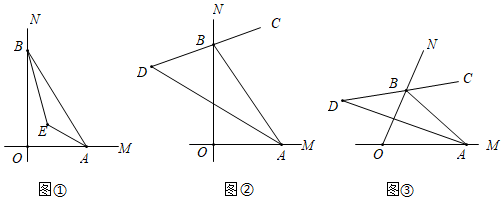
（問題思考）
（1）如圖①，AE、BE分別是∠BAO和∠ABO的平分線，隨著點A、點B的運動，∠AEB=．
（2）如圖②，若BC是∠ABN的平分線，BC的反向延長線與∠OAB的平分線交于點D．
①若∠BAO=70°，則∠D=°．
②隨著點A、B的運動，∠D的大小會變嗎？如果不會，求∠D的度數；如果會，請說明理由；
（問題拓展）
（3）在圖②的基礎上，如果∠MON=α，其余條件不變，隨著點A、B的運動（如圖③），∠D=．（用含α的代數式表示）發布：2025/6/3 5:0:1組卷：4250引用：14難度：0.5