在平面直角坐標系中，拋物線y=x2+bx+c與x軸交于A、B兩點且經過點C，已知A點坐標為（-1，0）．C點坐標為（4，5）．
（1）求拋物線的解析式；
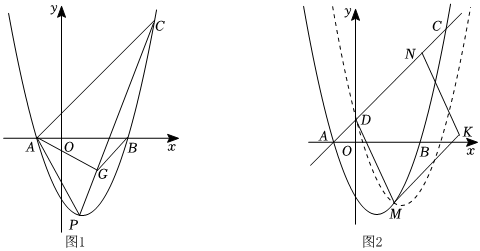
（2）如圖1，點P為第四象限內拋物線上一個動點，連接AC、AP，PC，過點B作BG∥AC交PC于點G，連接AG．請求出△APG面積的最大值以及此時點P的坐標；
（3）如圖2，將拋物線y=x2+bx+c沿射線AC方向平移2個單位長度得到新拋物線y'，記y與y'的交點為M，點D是直線AC與y軸的交點，點N為直線AC上一點，點K為平面內一點，若以D、M、K、N為頂點的四邊形是菱形且DM為菱形的邊，請直接寫出點K的坐標并選擇其中一個坐標寫出求解過程．
2
【考點】二次函數綜合題．
【答案】（1）y=x2-2x-3；
（2）△APG面積的最大值為，P（，-）；
（3）K點坐標為（-4，3）或（2+，-3+）或（2-，-3-）．
（2）△APG面積的最大值為
45
8
3
2
15
4
（3）K點坐標為（-4，3）或（2+
10
10
10
10
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/12 8:0:9組卷：581引用：1難度：0.2
相似題
-
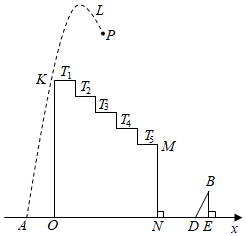1．如圖是某同學正在設計的一動畫示意圖，x軸上依次有A，O，N三個點，且AO=2，在ON上方有五個臺階T1～T5（各拐角均為90°），每個臺階的高、寬分別是1和1.5，臺階T1到x軸距離OK=10．從點A處向右上方沿拋物線L：y=-x2+4x+12發出一個帶光的點P．
（1）求點A的橫坐標，且在圖中補畫出y軸，并直接指出點P會落在哪個臺階上；
（2）當點P落到臺階上后立即彈起，又形成了另一條與L形狀相同的拋物線C，且最大高度為11，求C的解析式，并說明其對稱軸是否與臺階T5有交點；
（3）在x軸上從左到右有兩點D，E，且DE=1，從點E向上作EB⊥x軸，且BE=2．在△BDE沿x軸左右平移時，必須保證（2）中沿拋物線C下落的點P能落在邊BD（包括端點）上，則點B橫坐標的最大值比最小值大多少？
[注：（2）中不必寫x的取值范圍]發布：2025/5/24 17:30:1組卷：2754引用：4難度：0.1 -
2．如圖，拋物線y=ax2+bx+c（a≠0）與x軸交于A、B兩點，點A在點B的左邊，與y軸交于點C，點A的坐標為（-2，0），AO：CO：BO=1：2：3．
（1）如圖1，求拋物線的解析式；
（2）如圖1，點D在直線BC上方的拋物線上運動（不含端點B、C），連接DC、DB，當四邊形ABDC面積最大時，求出面積最大值和點D的坐標；
（3）如圖2，將（1）中的拋物線向右平移，當它恰好經過原點時，設原拋物線與平移后的拋物線交于點E，連接BE．點M為原拋物線對稱軸上一點，N為平面內一點，以B、E、M、N為頂點的四邊形是矩形時，若直線OK平分這個矩形面積，請直接寫出直線OK的解析式．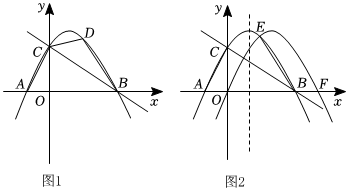
發布：2025/5/24 16:30:1組卷：255引用：1難度：0.1 -
3．已知：如圖1，二次函數y=ax2+4ax+
的圖象交x軸于A，B兩點（A在B的左側），過點A的直線y=kx+3k（k＞34）交該二次函數的圖象于另一點C（x1，y1），交y軸于M．14
（1）直接寫出A點坐標，并求該二次函數的解析式；
（2）過點B作BD⊥AC交AC于D，若M（0，3）且點Q是線段DC上的一個動點，求出當△DBQ與△AOM相似時點Q的坐標：3
（3）設P（-1，-2），圖2中連接CP交二次函數的圖象于另一點E（x2，y2），連接AE交y軸于N，請你探究OM?ON的值的變化情況，若變化，求其變化范圍；若不變，求其值．
發布：2025/5/24 16:30:1組卷：160引用：3難度：0.3