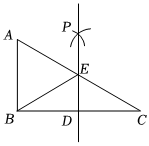
如圖，已知在Rt△ABC中，∠ABC=90°，點D是BC邊的中點，分別以B．C為圓心，大于線段BC長度一半的長為半徑畫弧，兩弧在直線BC上方的交點為P，直線PD交AC于點E，連接BE，則下列結論：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④EB=EC中，其中正確的結論有（ ）
【考點】作圖—基本作圖；線段垂直平分線的性質．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/4 8:0:8組卷：20引用：1難度：0.5
相似題
-
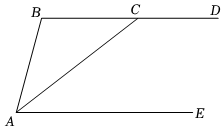1．如圖，已知BD∥AE，AC平分∠BAE．
（1）使用尺規完成基本作圖：作∠ABD的角平分線，交AC于O，交AE于F，連接CF（保留作圖痕跡，不寫作法，不下結論）
（2）求證：四邊形ABCF為菱形．（請補全下面的證明過程）
證明：∵AC平分∠BAE，
∴．
又∵BD∥AE，
∴，
∴∠BAC=∠BCA，
∴AB=CB．
同理可得：．
∴BC=AF．
又∵，
∴四邊形ABCF為平行四邊形，
∵BA=BC，
∴四邊形ABCF為菱形．發布：2025/6/13 3:30:1組卷：55引用：4難度：0.6 -
2．如圖，在△ABC中，∠C=90°，∠B=30°，以A為圓心，適當長為半徑畫弧，交AB于點M，交AC于點N．再分別以M，N為圓心，大于MN的長為半徑畫弧，兩弧在∠BAC內部交于點P．連接AP并延長，交BC于點D．有下列說法：①線段AD是∠BAC的平分線；②∠ADC=60°③點D到AB邊的距離與DC的長相等；④S△DAC：S△ABC=1：3．其中正確結論的個數是（ ）12發布：2025/6/13 6:30:2組卷：220引用：6難度：0.5 -
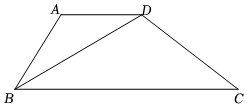3．如圖，在四邊形ABCD中，AB=AD，AD∥BC．
（1）用尺規作∠BAD的角平分線AF，分別交BD、BC于點E、F；（保留作圖痕跡，不寫作法）
（2）證明：AD=BF，根據已有證明過程完成填空．
證明：∵AF平分∠BAD
∴
∵AD∥BC
∴
∴
∴AB=BF
∵
∴AD=BF發布：2025/6/13 7:0:2組卷：171引用：3難度：0.7