如圖1，在矩形ABCD中，AB=3，AD=6，點E在邊BC上，且BE=2．動點P從點E出發(fā)，沿折線EB-BA-AD以每秒1個單位長度的速度運動，作∠PEQ=90°，EQ交邊AD或邊DC于點Q，連接PQ．當點Q與點C重合時，點P停止運動．設點P的運動時間為t秒．（t＞0）
（1）當點P和點B重合時，直接寫出點P的運動時間為 22秒和線段PQ的長為 1313；
（2）當點Q和點D重合時，求線段PQ的長；
（3）如圖2，當點P在邊AD上運動時，求證：PEEQ的值為定值．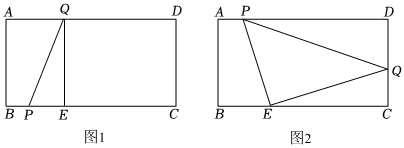
13
13
PE
EQ
【考點】相似形綜合題．
【答案】2；
13
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/10/2 13:0:1組卷：148引用：1難度：0.3
相似題
-
1．我們可以通過面積運算的方法，得到等腰三角形底邊上的任意一點到兩腰的距離之和與一腰上的高之間的數(shù)量關系，并利用這個關系解決相關問題．
（1）如圖一，在等腰△ABC中，AB=AC，BC邊上有一點D，過點D作DE⊥AB于E，DF⊥AC于F，過點C作CG⊥AB于G．利用面積證明：DE+DF=CG．
（2）如圖二，將矩形ABCD沿著EF折疊，使點A與點C重合，點B落在B'處，點G為折痕EF上一點，過點G作GM⊥FC于M，GN⊥BC于N．若BC=8，BE=3，求GM+GN的長．
（3）如圖三，在四邊形ABCD中，E為線段BC上的一點，EA⊥AB，ED⊥CD，連接BD，且=ABCD，BC=AEDE，CD=3，BD=6，求ED+EA的長．51
發(fā)布：2025/5/22 8:30:1組卷：1641引用：4難度：0.3 -
2．綜合與實踐
我們在沒有量角器或三角尺的情況下，用折疊特殊矩形紙片的方法進行如下操作也可以得到幾個相似的含有30°角的直角三角形．
實踐操作：第一步：如圖①，矩形紙片ABCD的邊長AB=，將矩形紙片ABCD對折，使點D與點A重合，點C與點B重合，折痕為EF，然后展開，EF與CA交于點H．3
第二步：如圖②，將矩形紙片ABCD沿過點C的直線再次折疊，使CD落在對角線CA上，點D的對應點D'恰好與點H重合，折痕為CG，將矩形紙片展平，連接GH．
問題解決：
（1）在圖②中，sin∠ACB=，=；EGCG
（2）在圖②中，CH2=CG?；從圖②中選擇一條線段填在空白處，并證明你的結論；
拓展延伸：
（3）將上面的矩形紙片ABCD沿過點C的直線折疊，點D的對應點D'落在矩形的內(nèi)部或一邊上，設∠DCD'=a,若0°＜a≤90°，連接D'A，D'A的長度為m,則m的取值范圍是 ．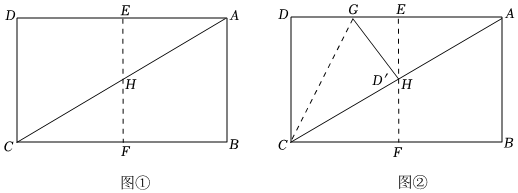
發(fā)布：2025/5/22 9:30:1組卷：681引用：7難度：0.1 -
3．如圖，在矩形ABCD中，AB=10，BC=6，E是AD上一點，AE=2．F是AB上的動點，連接EF，G是EF上一點，且為常數(shù)，k≠0）．分別過點F、G作AB、EF的垂線相交于點P．設AF的長為x,PF的長為y.GFEF=k（k
（1）若，則y的值是 ；k=12，x=4
（2）求y與x之間的函數(shù)表達式；
（3）在點F從點A到點B的整個運動過程中，若線段CD上存在點P，則k的值應滿足什么條件？直接寫出k的取值范圍．發(fā)布：2025/5/22 8:30:1組卷：2225引用：1難度：0.3