探究：是否存在一個(gè)新矩形，使其周長(zhǎng)和面積為原矩形的2倍、12倍、k倍．
（1）若該矩形為正方形，是否存在一個(gè)正方形，使其周長(zhǎng)和面積都為邊長(zhǎng)為2的正方形的2倍？不存在不存在（填“存在”或“不存在”）．
（2）繼續(xù)探究，是否存在一個(gè)矩形，使其周長(zhǎng)和面積都為長(zhǎng)為3，寬為2的矩形的2倍？
同學(xué)們有以下思路：
①設(shè)新矩形長(zhǎng)和寬為x、y,則依題意x+y=10，xy=12，聯(lián)立x+y=10 xy=12
得x2-10x+12=0，再探究根的情況；
根據(jù)此方法，請(qǐng)你探究是否存在一個(gè)矩形，使其周長(zhǎng)和面積都為原矩形的12倍；
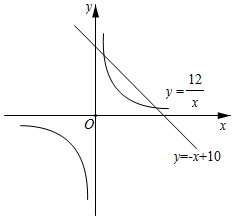
②如圖也可用反比例函數(shù)與一次函數(shù)證明l1：y=-x+10，l2：y=12x，那么，
a.是否存在一個(gè)新矩形為原矩形周長(zhǎng)和面積的2倍？存在存在．
b.請(qǐng)?zhí)骄渴欠裼幸恍戮匦沃荛L(zhǎng)和面積為原矩形的12，若不存在，用圖象表達(dá)；
c.請(qǐng)直接寫(xiě)出當(dāng)結(jié)論成立時(shí)k的取值范圍：k≥2425k≥2425．
1
2
x + y = 10 |
xy = 12 |
1
2
12
x
1
2
24
25
24
25
【考點(diǎn)】反比例函數(shù)綜合題．
【答案】不存在；存在；k≥
24
25
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/25 12:0:2組卷：4070引用：4難度：0.3
相似題
-
1．背景：點(diǎn)A在反比例函數(shù)y=
（k＞0）的圖象上，AB⊥x軸于點(diǎn)B，AC⊥y軸于點(diǎn)C，分別在射線AC，BO上取點(diǎn)D，E，使得四邊形ABED為正方形．如圖1，點(diǎn)A在第一象限內(nèi)，當(dāng)AC=4時(shí)，小李測(cè)得CD=3．kx
探究：通過(guò)改變點(diǎn)A的位置，小李發(fā)現(xiàn)點(diǎn)D，A的橫坐標(biāo)之間存在函數(shù)關(guān)系．請(qǐng)幫助小李解決下列問(wèn)題．
（1）求k的值．
（2）設(shè)點(diǎn)A，D的橫坐標(biāo)分別為x,z,將z關(guān)于x的函數(shù)稱(chēng)為“Z函數(shù)”．如圖2，小李畫(huà)出了x＞0時(shí)“Z函數(shù)”的圖象．
①求這個(gè)“Z函數(shù)”的表達(dá)式；
②補(bǔ)畫(huà)x＜0時(shí)“Z函數(shù)”的圖象；
③并寫(xiě)出這個(gè)函數(shù)的性質(zhì)（兩條即可）．
發(fā)布：2025/5/26 1:0:1組卷：438引用：4難度：0.4 -
2．如圖，在平面直角坐標(biāo)系xOy中，一次函數(shù)y=x+34的圖象與反比例函數(shù)y=32（x＞0）的圖象相交于點(diǎn)A（a,3），與x軸相交于點(diǎn)B．kx
（1）求反比例函數(shù)的表達(dá)式；
（2）過(guò)點(diǎn)A的直線交反比例函數(shù)的圖象于另一點(diǎn)C，交x軸正半軸于點(diǎn)D，當(dāng)△ABD是以BD為底的等腰三角形時(shí)，求直線AD的函數(shù)表達(dá)式及點(diǎn)C的坐標(biāo)．發(fā)布：2025/5/25 23:30:1組卷：4150引用：15難度：0.5 -
3．如圖，一次函數(shù)y=-x+5與反比例函數(shù)的圖象交于點(diǎn)A，B．y=4x（x≠0）
（1）求點(diǎn)A，B的坐標(biāo)；
（2）觀察圖象寫(xiě)出不等式的解集；-x+5＞4x
（3）若位于第三象限的點(diǎn)M在反比例函數(shù)的圖象上，且△MAB是以AB為底的等腰三角形，請(qǐng)直接寫(xiě)出點(diǎn)M的坐標(biāo)和△MAB的面積．y=4x（x≠0）發(fā)布：2025/5/25 23:30:1組卷：405引用：2難度：0.4
相關(guān)試卷