綜合與實踐
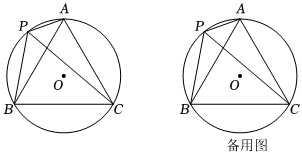
數學活動課上，老師出示了一個問題：如圖，已知三只螞蟻A、B、C在半徑為1的⊙O上靜止不動，第四只螞蟻P在⊙O上的移動，并始終保持∠APC=∠CPB=60°．
（1）請判斷△ABC的形狀；
“數學希望小組”很快得出結論，請你回答這個結論：△ABC是 等邊等邊三角形；
（2）“數學智慧小組”繼續研究發現：當第四只螞蟻P在⊙O上的移動時，線段PA、PB、PC三者之間存在一種數量關系：請你寫出這種數量關系：PC=PA+PBPC=PA+PB，并加以證明；
?
（3）“數學攀峰小組”突發奇想，深入探究發現：若第五只螞蟻M同時隨著螞蟻P的移動而移動，且始終位于線段PC的中點，在這個運動過程中，線段BM的長度一定存在最小值，請你求出線段BM的最小值是 72-1272-12（不寫解答過程，直接寫出結果）．
7
2
-
1
2
7
2
-
1
2
【考點】圓的綜合題．
【答案】等邊；PC=PA+PB；
7
2
-
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/3 8:0:9組卷：624引用：2難度：0.2
相似題
-
1．旋轉的圖形帶來結論的奧秘．已知△ABC，將△ABC繞點A逆時針旋轉得到△AB'C'．
初步探索 素材1： 
如圖①，連接對應點BB'，CC'，則．BB′CC′=ABAC素材2： 
如圖②，以A為圓心，BC邊上的高AD為半徑作⊙A，則B'C'與⊙A相切．問題解決 （1）（ⅰ）請證明素材1所發現的結論．
（ⅱ）如圖2，過點A作AD'⊥B'C'，垂足為D'．證明途徑可以用下面的框圖表示，請填寫其中的空格．
深入研究 （2）在Rt△ABC滿足∠A=90°， ，AB=5，M是AC的中點，△ABC繞點M逆時針旋轉得△A'B'C'．AC=25
（ⅰ）如圖③，當邊B'C'恰好經過點C時，連接BB'，則BB'的長為 ．
（ⅱ）若邊B'C'所在直線l恰好經過點B，于圖④中利用無刻度的直尺和圓規作出直線l.（只保留作圖痕跡）
（3）在（2）的條件下，如圖⑤，在旋轉過程中，直線BB'，CC'交于點P，求BP的最大值為 ．
發布：2025/5/22 22:30:1組卷：204引用：1難度：0.1 -
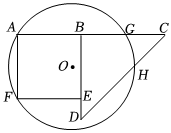2．如圖，點G在線段AC上，AG=6，點B是線段AG上一動點，以AB為邊向下方作正方形ABEF，以BC為腰向下方作等腰直角三角形BCD，∠CBD=Rt∠，當AB＜BC時，2BG-DE=4．
（1）如下表，某同學分別用特殊值法和一般法求CG的長，請你將解答過程補充完整．
（2）過點A，F，G的⊙O交邊CD于點H．探究1 假設BG=3，求CG的長． 探究2 設BG=x,求CG的長． 解：… 解：…
①連結GH，FH，若△CGH是等腰三角形，求AB的長．
②當⊙O與邊CD有兩個交點時，求AB的取值范圍．發布：2025/5/22 23:0:1組卷：463引用：3難度：0.2 -
3．已知：四邊形ABCD內接于⊙O，AC、BD即相交于點F，連接OC，∠BCO=∠ABD．
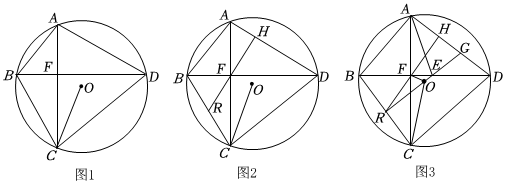
（1）如圖1，求證：AC⊥BD；
（2）如圖2，過點F作FH⊥AD于點H，延長HF交BC于點R．求證：BR=CR；
（3）如圖3，在（2）的條件下，點E、點G分別是FD，AD上的點，連接AE、EG、OR，∠ADB=2∠CAE，，EF=2，EG=DG=154，求⊙O的半徑．tan∠FOR=76發布：2025/5/22 23:30:1組卷：131引用：1難度：0.3