知識探究：
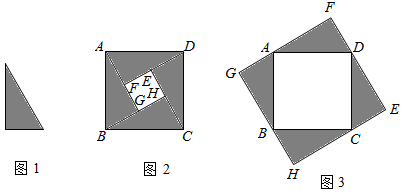
如圖1是兩直角邊長分別為m,n（m＞n）的直角三角形，如果用四個與圖1完全一樣的直角三角形可以拼成如圖2和圖3的幾何圖形．其中圖2和圖3的四邊形ABCD、四邊形EFGH都是正方形．請你根據幾何圖形部分與整體的關系完成第（1）（2）題．
請選擇（m+n）2，（m-n）2，mn中的有關代數式表示：
圖2中正方形ABCD的面積：（m-n）2+2mn（m-n）2+2mn．
圖3中正方形ABCD的面積：（m+n）2-2mn（m+n）2-2mn．
（2）請你根據題（1），寫出下列三個代數式：（m+n）2，（m-n）2，mn之間的等量關系（m-n）2=（m+n）2-4mn或者（m+n）2=（m-n）2+4mn.（m-n）2=（m+n）2-4mn或者（m+n）2=（m-n）2+4mn.．
知識應用：
（3）根據（2）題中的等量關系，解決如下問題：
①已知：a-b=5，ab=-6，求：（a+b）2的值；
②已知：a＞0，a-1a=5，求：a+1a的值．
1
a
5
1
a
【答案】（m-n）2+2mn；（m+n）2-2mn；（m-n）2=（m+n）2-4mn或者（m+n）2=（m-n）2+4mn．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：899引用：5難度：0.5
相似題
-
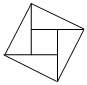1．如圖是一個“趙爽弦圖”，它是由四個全等的直角三角形圍成一個大正方形，中空的部分也是一個小正方形，若大正方形的邊長為7，小正方形的邊長為3，直角三角形的兩直角邊分別為a,b,則ab的值為 ．發布：2025/6/7 11:0:1組卷：255引用：5難度：0.7 -
2．綜合與實踐：
問題情境
學過幾何的人都知道勾股定理，它是幾何中一個比較重要的定理，應用十分廣泛．迄今為止，關于勾股定理的證明方法已有400多種．在學習了《勾股定理》和《實數》后，某班同學以“已知三角形三邊的長度，求三角形面積”為主題開展了數學活動．
操作發現
如圖1是6×6的正方形網格，每個小正方形的邊長均為1，每個小正方形的頂點稱為格點．在圖1中畫出△ABC，其頂點A，B，C都是格點，同時構造正方形BDEF，使它的頂點都在格點上，且它的邊DE，EF分別經過點C，A，他們借助此圖求出了△ABC的面積．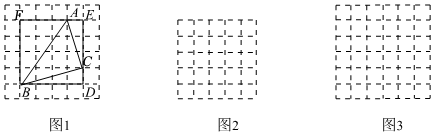
（1）在圖1中，所畫出的△ABC的三邊長分別是AB=，BC=，AC=；△ABC的面積為 ．
實踐探究
（2）在圖2所示的正方形網格中畫出△DEF（頂點都在格點上），使DE=，DF=5，EF=13，并寫出△DEF的面積．20
繼續探究
（3）若△ABC中有兩邊的長分別為a,2a（a＞0），且△ABC的面積為2a2，試運用構圖法在圖3的正方形網格（每個小正方形的邊長為a）中畫出所有符合題意的△ABC（全等的三角形視為同一種情況），并求出它的第三條邊長填寫在橫線上 ．10發布：2025/6/7 8:0:1組卷：1062引用：7難度：0.4 -
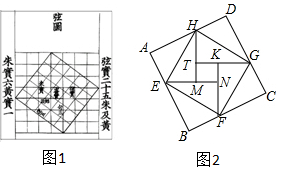3．我國漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”，后人稱其為“趙爽弦圖”（如圖1所示）．圖2由弦圖變化得到，它是由八個全等的直角三角形拼接而成的記圖中正方形ABCD，正方形EFGH，正方形MNKT的面積分別為S1，S2，S3，若EF=4，則S1+S2+S3的值是（ ）發布：2025/6/7 4:0:1組卷：837引用：8難度：0.5