已知：四邊形ABCD，連接AC，AD=CD，∠DAC=∠ABC，∠DCA=∠BAC，AD∥BC．
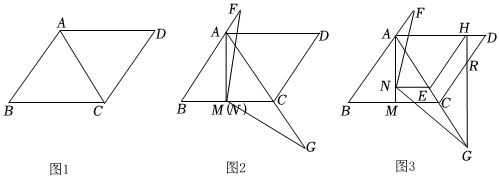
（1）如圖1，求證：△ABC是等邊三角形；
（2）過點A作AM⊥BC于點M，點N為AM上一點（不與點A重合），∠FNG=120°，∠FNG的邊NF交BA的延長線于點F，另一邊NG交AC的延長線于點G，如圖2，點N與點M重合時，求證：NF=NG；
（3）如圖3，在（2）的條件下，點N不與點M重合，過點N作NE⊥AM，交AC于點E，EN：CM=3：4，AF=3，CG=4，點H為AD上一點，連接EH、GH，GH交CD于點R，EH=EG，求DR的長．
【考點】四邊形綜合題．
【答案】（1）證明見解析；
（2）證明見解析；
（3）4．
（2）證明見解析；
（3）4．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/29 15:30:1組卷：155引用：1難度：0.1
相似題
-
1．在第九章中我們研究了幾種特殊四邊形，請根據你的研究經驗來自己研究一種特殊四邊形——箏形．
初識定義：兩組鄰邊分別相等的四邊形是箏形．
（1）類比你學過的特殊四邊形的性質，通過觀察、測量、折疊、證明等操作活動，對如圖1的箏形ABCD（AB=AD，BC=CD）的性質進行探究，以下判斷正確的有 ．（填序號）．
①AC、BD互相平分； ②AC⊥BD；
③AC平分∠BAD和∠BCD；
④∠ABC=∠ADC；⑤∠BAD+∠BCD=180°．
（2）性質運用：如圖2，在箏形ABCD中，AB=BC，AD=CD，點P是對角線BD上一點，過P分別作AD、CD垂線，垂足分別為點M、N．若∠ADC=90°，求證：四邊形PNDM是正方形．
（3）如圖3，在箏形ABCD中，AB=AD=15，BC=DC=13，AC=14，則箏形ABCD的面積是 ．發布：2025/6/4 11:0:2組卷：552引用：3難度：0.2 -
2．動態幾何問題是由點動、線動、形動而構成的，需要用運動與變化的眼光去觀察和研究圖形．有時借助特殊的四邊形常常能幫助我們化“動”為“靜”．
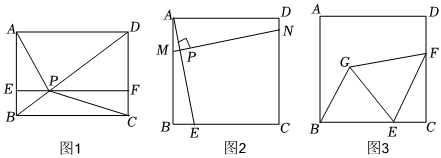
（1）問題1：如圖1，點P為矩形ABCD對角線BD上一動點，過點P作EF∥BC，分別交AB，CD于點E，F．若△AEP的面積為S1，△CFP的面積為S2，則S1與S2的數量關系是S1S2（填“＞”、“＜”或“=”）；
（2）問題2：如圖2，在正方形ABCD中，E為邊BC上一動點（不與點B、C重合），垂直于AE的一條直線MN分別交AB、AE、CD于點M、P、N．判斷線段DN、MB、EC之間的數量關系，并說明理由．
（3）問題3：如圖3，正方形ABCD的邊長為4，E為BC上一點，且BE=3，F為CD邊上的一個動點，連接EF，以EF為邊向左側作等邊△EFG，連接BG，則BG的最小值為 ．發布：2025/6/4 10:0:1組卷：468引用：5難度：0.4 -
3．如圖，點O為矩形ABCD的對稱中心，AB=10cm,BC=12cm.點E，F，G分別從A，B，C三點同時出發，沿矩形的邊按逆時針方向勻速運動，點E的運動速度為1cm/s,點F的運動速度為3cm/s,點G的運動速度為xcm/s.當點F到達點C（即點F與點C重合）時，三個點隨之停止運動．在運動過程中，△EBF關于直線EF的對稱圖形是△EB'F，設點E，F，G運動的時間為t（單位：s）．
（1）當t=s時，四邊形EBFB'為正方形；
（2）當x為何值時，以點E，B，F為頂點的三角形與以點F，C，G為頂點的三角形可能全等？
（3）是否存在實數t,使得點B'與點O重合？若存在，求出t的值；若不存在，請說明理由．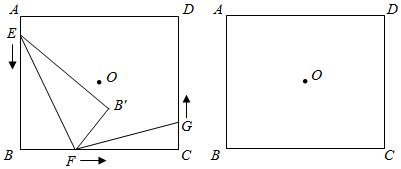
發布：2025/6/4 10:0:1組卷：1184引用：5難度：0.1