2022-2023學(xué)年黑龍江省哈爾濱市香坊區(qū)八年級（上）期末數(shù)學(xué)試卷（五四學(xué)制）

一、選擇題（每小題3分，共計(jì)30分）

• 1．在

  1

  x

  ，

  1

  2022

  ，

  x

  2

  +

  1

  2

  ，

  3

  x

  x

  +

  y

  中，分式的個(gè)數(shù)為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：199引用：1難度：0.9

  解析

• 2．下面的圖案中，不是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：176引用：9難度：0.9

  解析

• 3．下列二次根式中屬于最簡二次根式的是（　　）

  A． 24

  B． 16

  C． 7

  D． 0 . 2
  組卷：497引用：10難度：0.9

  解析

• 4．下列運(yùn)算一定正確的是（　　）

  A．a(chǎn)9÷a3=a3	B．a(chǎn)3+a3=a6
  C．（a-b）2=a2-b2	D．（a2）3=a6
  組卷：29引用：1難度：0.8

  解析

• 5．如果把分式

  2

  x

  3

  x

  -

  2

  y

  中的x,y都擴(kuò)大為原來的3倍，那么分式的值（　　）

  A．?dāng)U大3倍	B．不變
  C．縮小為原來的 1 3	D．?dāng)U大到原來的9倍
  組卷：335引用：3難度：0.7

  解析

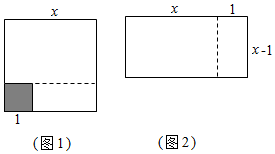• 6．如圖1，將邊長為x的大正方形剪去一個(gè)邊長為1的小正方形（陰影部分），并將剩余部分沿虛線剪開，得到兩個(gè)長方形，再將這兩個(gè)長方形拼成圖2所示長方形．這兩個(gè)圖能解釋下列哪個(gè)等式（　　）

  A．x2-2x+1=（x-1）2	B．x2-1=（x+1）（x-1）
  C．x2+2x+1=（x+1）2	D．x2-x=x（x-1）
  組卷：3958引用：81難度：0.6

  解析

• 7．下列說法一定正確的是（　　）

  A．有兩個(gè)角相等的三角形一定是等邊三角形

  B．有一個(gè)角是60°的等腰三角形是等邊三角形

  C．等腰三角形的對稱軸是頂角的角平分線

  D．如果兩個(gè)三角形全等，那么它們必是關(guān)于某條直線成軸對稱的圖形
  組卷：71引用：3難度：0.6

  解析

• 8．若x+m與x+3的乘積中不含x的一次項(xiàng)，則m的值為（　　）

  A．0

  B．1

  C．3

  D．-3
  組卷：714引用：16難度：0.9

  解析

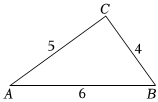• 9．古希臘幾何學(xué)家海倫在他的著作《度量》中，給出了計(jì)算三角形面積的海倫公式，若一個(gè)三角形三邊長分別為a、b、c,記p=

  a

  +

  b

  +

  c

  2

  ，三角形的面積為s=

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  ，如圖，請你利用海倫公式計(jì)算△ABC的面積為（　　）

  A． 15 2 7

  B．5 7

  C． 15 4 7

  D．3 7
  組卷：335引用：4難度：0.7

  解析

三、解答題（其中21-22題各7分，23-24題各8分，25-27題各10分，共計(jì)60分）

• 26．已知：四邊形ABCD，連接AC，AD=CD，∠DAC=∠ABC，∠DCA=∠BAC，AD∥BC．
  
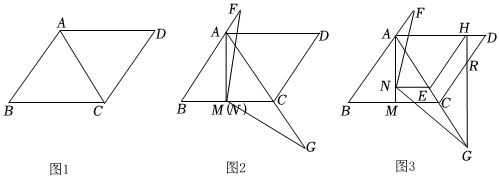
  （1）如圖1，求證：△ABC是等邊三角形；
  （2）過點(diǎn)A作AM⊥BC于點(diǎn)M，點(diǎn)N為AM上一點(diǎn)（不與點(diǎn)A重合），∠FNG=120°，∠FNG的邊NF交BA的延長線于點(diǎn)F，另一邊NG交AC的延長線于點(diǎn)G，如圖2，點(diǎn)N與點(diǎn)M重合時(shí)，求證：NF=NG；
  （3）如圖3，在（2）的條件下，點(diǎn)N不與點(diǎn)M重合，過點(diǎn)N作NE⊥AM，交AC于點(diǎn)E，EN：CM=3：4，AF=3，CG=4，點(diǎn)H為AD上一點(diǎn)，連接EH、GH，GH交CD于點(diǎn)R，EH=EG，求DR的長．
  組卷：155引用：1難度：0.1

  解析

• 27．已知：在平面直角坐標(biāo)系中，點(diǎn)A（a,0），點(diǎn)C（0，b），其中（a+1）²=0，

  b

  -

  2

  =0．
  
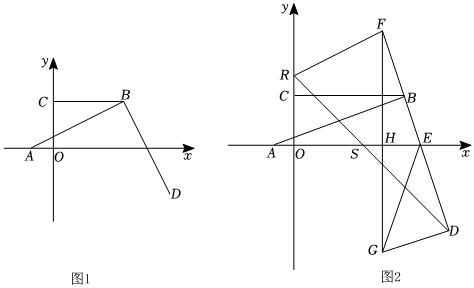
  （1）分別求a、b的值；
  （2）如圖1，點(diǎn)B在第一象限內(nèi)，連接AB、BC，BC⊥y軸，點(diǎn)D在第四象限內(nèi)，連接BD，BD⊥BA，BD=BA，設(shè)BC=t,點(diǎn)D的縱坐標(biāo)是d,請你用含有t的代數(shù)式表示d；
  （3）如圖2，在（2）的條件下，DB交x軸于點(diǎn)E，連接DS并延長交y軸于點(diǎn)R，延長DB至點(diǎn)F，連接FR，過點(diǎn)F作FH⊥OE于點(diǎn)H，延長FH交過點(diǎn)D垂直于BD的垂線于點(diǎn)G，連接EG，若∠DEG+2∠GEH=180°，點(diǎn)R的坐標(biāo)為（0，n），點(diǎn)F（m,

  1

  2

  m+n），求點(diǎn)G的坐標(biāo)．
  組卷：88引用：1難度：0.1

  解析