綜合與實踐
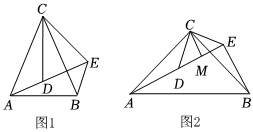
（1）問題發現：如圖1，△ACB和△DCE均為等腰三角形，AC=BC，DC=EC，∠ACB=∠DCE，點A、D、E在同一條直線上，連接BE．
①求證：AD=BE；
②若∠ACB=50°，則∠AEB的度數為 50°50°．
（2）類比探究：如圖2，△ACB和△DCE均為等腰直角三角形，∠ACB=∠DCE=90°，點A、D、E在同一條直線上，CM為△DCE中DE邊上的高，連接BE．
①∠AEB的度數為 90°90°；
②線段AE、BE與2CM之間的數量關系為 AE=BE+2CMAE=BE+2CM．
（3）拓展延伸：在（2）的條件下，若BE=2，CM=1，則四邊形ABEC的面積為 66．
【答案】50°；90°；AE=BE+2CM；6
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/29 14:30:2組卷：159引用：3難度：0.5
相似題
-
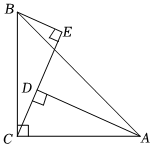1．如圖，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，若AD=3，BE=1，則DE=（ ）發布：2025/5/31 6:30:1組卷：3643引用：27難度：0.9 -
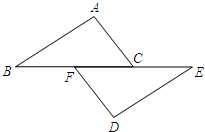2．如圖，點B、F、C、E在一條直線上，AC=FD，AC∥FD，∠A=∠D．
（1）求證：△ABC≌△DEF；
（2）若BE=10，FC=4，求CE的長度．發布：2025/5/31 6:30:1組卷：345引用：5難度：0.5 -
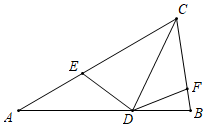3．在△ABC中，AB=AC，∠A=36°，CD平分∠ACB交AB于D，E，F在AC，BC上，且∠EDF=108°．
（1）求∠ADC的度數；
（2）求證：AE+BF=BC．發布：2025/5/31 6:30:1組卷：3947引用：7難度：0.5