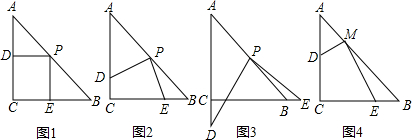
操作：在△ABC中，AC=BC=2，∠C=90°，將一塊等腰直角三角板的直角頂點放在斜邊AB的中點P處，將三角板繞點P旋轉，三角板的兩直角邊分別交射線AC、CB于D、E兩點．圖1，2，3是旋轉三角板得到的圖形中的3種情況．
研究：
（1）三角板繞點P旋轉，觀察線段PD和PE之間有什么數量關系，并結合圖2加以證明；
（2）三角板繞點P旋轉，△PBE是否能成為等腰三角形？若能，指出所有情況（即寫出△PBE為等腰三角形時CE的長）；若不能，請說明理由；
（3）若將三角板的直角頂點放在斜邊AB上的M處，且AM：MB=1：3，和前面一樣操作，試問線段MD和ME之間有什么數量關系？并結合圖4加以證明．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1439引用：53難度：0.1
相似題
-
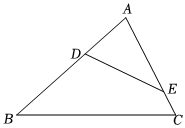1．如圖，點D、E分別在△ABC邊AB、AC上，，且∠AED=∠B，那么ABAD=AECE=3的值為（ ）ADAC發布：2025/5/24 9:30:2組卷：474引用：3難度：0.5 -
2．如圖，AB=10，點C是射線BQ上的動點，連結AC，作CD⊥AC，CD=AC，動點E在AB延長線上，tan∠QBE=3，連結CE，DE，當CE=DE，CE⊥DE時，BE的長是 ．發布：2025/5/24 8:30:1組卷：2438引用：4難度：0.3 -
3．如圖，平行四邊形ABCD中，點E在CD邊上，連接BE，∠ABE=60°，F在BE上，AF=CE，∠BAF=∠CBE，若AD=7，AB=6，則BF=．發布：2025/5/24 8:30:1組卷：302引用：2難度：0.5