綜合與探究；問題情境：
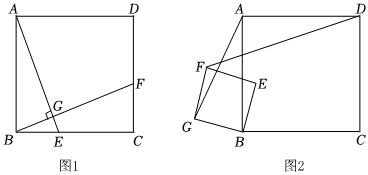
如圖，正方形ABCD的邊長為12，點E在BC邊上運動．
探究發現：
（1）如圖1，當BE=5時，連接AE，過點B作BF⊥AE于點G，交CD于點F，請求出線段BG和BF的長度；
（2）如圖2，以BE為邊作正方形BEFG，并把正方形BEFG繞點B逆時針旋轉，連接AG和DF，發現DF與AG之間存在數量關系，請寫出它們的數量關系并證明．
【答案】（1）BG=，BF=13；
（2）DF=AG，理由見解析過程．
60
13
（2）DF=
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/26 8:0:9組卷：77引用：1難度：0.6
相似題
-
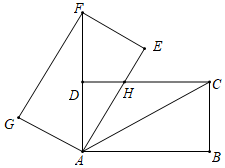1．如圖，將矩形ABCD繞點A旋轉至矩形AEFG的位置，此時點D恰好與AF的中點重合，AE交CD于點H，若BC=2，則HC的長為．3發布：2025/5/24 21:0:1組卷：122引用：2難度：0.6 -
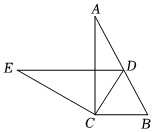2．如圖所示，把Rt△ABC繞點C按逆時針方向旋轉得到Rt△EDC，若點D恰好是邊AB的中點，BC=a,則點A運動到點E的位置時，所經過的路線長為（ ）發布：2025/5/24 21:30:1組卷：253引用：2難度：0.3 -
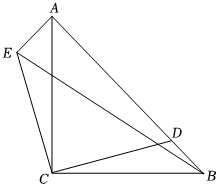3．如圖，在Rt△MBC中，∠ACB=90°，AC=BC，點D為AB邊上的一點，將△BCD繞點C逆時針旋轉90°得到△ACE，點B，D的對應點分別為點A，E，連結BE．
（1）求證：∠BCE+∠ACD=180°．
（2）當BC=3，BD=時，求BE的長．2發布：2025/5/24 21:30:1組卷：122引用：1難度：0.6