教材在探索平方差公式時利用了面積法，面積法除了可以幫助我們記憶公式，還可以直觀地推導或驗證公式，俗稱“無字證明”，例如，著名的趙爽弦圖（如圖①，其中四個直角三角形較大的直角邊長都為a,較小的直角邊長都為b,斜邊長都為c），大正方形的面積可以表示為c2，也可以表示為4×12ab+（a-b）2由此推導出重要的勾股定理：如果直角三角形兩條直角邊長為a,b,斜邊長為c,則a2+b2=c2．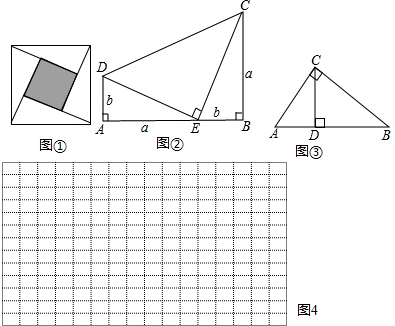
（1）圖②為美國第二十任總統伽菲爾德的“總統證法”，請你利用圖②推導勾股定理．
（2）如圖③，直角△ABC中，∠ACB=90°，AC=3cm,BC=4cm,則斜邊AB上的高CD的長為125125cm.
（3）試構造一個圖形，使它的面積能夠解釋（a+b）（a+2b）=a2+3ab+2b2，畫在如圖4的網格中，并標出字母a、b所表示的線段．
1
2
ab
+
（
a
-
b
）
2
12
5
12
5
【考點】勾股定理的證明．
【答案】
12
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：693引用：3難度：0.5
相似題
-
1．如圖，由四個全等的直角三角形拼成“趙爽弦圖”． Rt△ABF中，∠AFB=90°，AF=3，AB=5．四邊形EFGH的面積是．發布：2025/6/18 9:0:1組卷：190引用：4難度：0.7 -
2．在北京召開的國際數學家大會會標如圖所示，它是由四個相同的直角三角形與中間的小正方形拼成的一個大正方形，若大正方形的面積是13，小正方形的面積是1，直角三角形的較長直角邊為a,較短直角邊為b,則a4+b4的值為（ ）發布：2025/6/18 2:30:1組卷：750引用：3難度：0.9 -
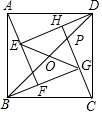3．如圖，四個全等的直角三角形拼成“趙爽弦圖”，得到正方形ABCD與正方形EFGH．連接EG，BD相交于點O，BD與HC相交于點P．若GO=GP，則的值是（ ）S正方形ABCDS正方形EFGH發布：2025/6/17 22:0:1組卷：5295引用：33難度：0.6