2019-2020學年河南省實驗文博學校八年級（上）開學數學試卷

一、填空題（5分×10=50分）

• 1．如果一個多邊形的內角和是1440°，那么這個多邊形是

   

  邊形．
  組卷：380引用：49難度：0.7

  解析

• 2．下列四種基本尺規作圖分別表示：①作一個角等于已知角；②作一個角的平分線；③做一條線段的垂直平分線；④過直線外一點作已知直線的垂線．則對應選項中做法錯誤的是

  ．
  
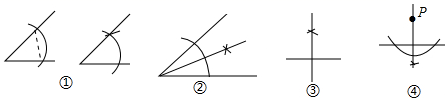  組卷：144引用：2難度：0.8

  解析

• 3．下列說法正確的是

  ．①同角或等角的余角相等；②角是軸對稱圖形，角平分線是它的對稱軸；③等腰三角形的平分線、底邊上的中線、底邊上的高重合，即“三線合一”；④必然事件發生的概率為1，不可能事件發生的概率為0．
  組卷：37引用：1難度：0.5

  解析

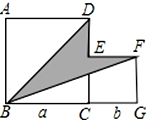• 4．如圖所示，兩個正方形的邊長分別為a和b,如果a+b=10，ab=20，那么陰影部分的面積是

   

  ．
  組卷：665引用：20難度：0.5

  解析

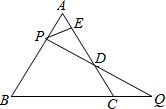• 5．如圖，過邊長為2的等邊△ABC的邊AB上點P作PE⊥AC于E，Q為BC延長線上一點，當PA=CQ時，連PQ交AC邊于D，則DE長為

  ．
  組卷：842引用：19難度：0.9

  解析

二、解答題（共70分）

• 14．教材在探索平方差公式時利用了面積法，面積法除了可以幫助我們記憶公式，還可以直觀地推導或驗證公式，俗稱“無字證明”，例如，著名的趙爽弦圖（如圖①，其中四個直角三角形較大的直角邊長都為a,較小的直角邊長都為b,斜邊長都為c），大正方形的面積可以表示為c²，也可以表示為4×

  1

  2

  ab

  +

  （

  a

  -

  b

  ）

  2

  由此推導出重要的勾股定理：如果直角三角形兩條直角邊長為a,b,斜邊長為c,則a²+b²=c²．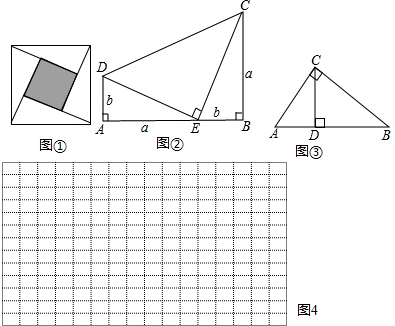
  （1）圖②為美國第二十任總統伽菲爾德的“總統證法”，請你利用圖②推導勾股定理．
  （2）如圖③，直角△ABC中，∠ACB=90°，AC=3cm,BC=4cm,則斜邊AB上的高CD的長為

   

  cm.
  （3）試構造一個圖形，使它的面積能夠解釋（a+b）（a+2b）=a²+3ab+2b²，畫在如圖4的網格中，并標出字母a、b所表示的線段．
  組卷：693引用：3難度：0.5

  解析

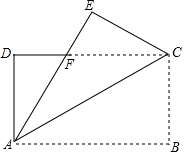• 15．如圖，長方形的紙片ABCD中，AD=3cm,AB=4cm,把該紙片沿直線AC折疊，點B落在點E處，AE交DC于點F．
  （1）圖中有等腰三角形嗎？說明理由．
  （2）求重疊部分（即△ACF）的面積．
  組卷：77引用：1難度：0.5

  解析