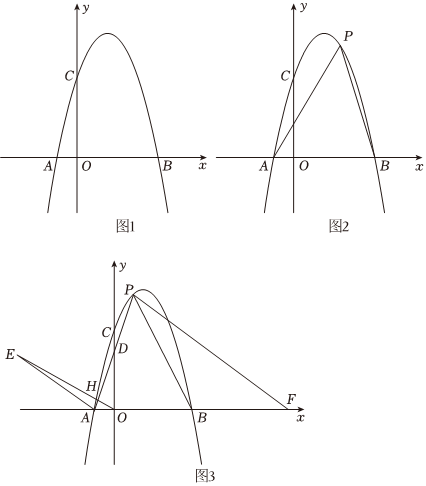
如圖1，在平面直角坐標(biāo)系中，O為坐標(biāo)原點(diǎn)，拋物線y=ax²+3x+c與x軸交于點(diǎn)A、B（A左B右），與y軸交于點(diǎn)C，直線y=-x+4經(jīng)過(guò)點(diǎn)B、C．
（1）求拋物線的解析式；
（2）如圖2，點(diǎn)P為第一象限內(nèi)拋物線上一點(diǎn)，連接PA，PB，設(shè)點(diǎn)P的橫坐標(biāo)為t,△PAB的面積為S，求S與t之間的函數(shù)關(guān)系式（不要求寫(xiě)出自變量t的取值范圍）；
（3）在（2）的條件下，如圖3，AP交y軸于點(diǎn)D，AD=DP，點(diǎn)F為x軸上點(diǎn)B右側(cè)一點(diǎn)，∠PAB-∠BPF=45°，將線段AB繞著點(diǎn)A逆時(shí)針旋轉(zhuǎn)至AE，AE∥PF，連接OE交拋物線于點(diǎn)H，求點(diǎn)H的坐標(biāo)．

【答案】（1）y=-x²+3x+4；
（2）S=-

；
（3）H（

181

，

181

）．

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。

發(fā)布：2024/9/6 9:0:9組卷：129引用：2難度：0.3

相似題

1．已知二次函數(shù)y=a（a+1）x²-（2a+1）x+1，其中a為正整數(shù)．
（1）若函數(shù)y的圖象與x軸相交于A、B兩點(diǎn)，求線段AB的長(zhǎng)；
（2）若a依次取1，2，…，2005時(shí)，函數(shù)y的圖象與x軸相交所截得的2005條線段分別為A₁B₁，A₂ B₂，…，A₂₀₀₅ B₂₀₀₅，試求這2005條線段長(zhǎng)之和．
發(fā)布：2025/5/28 8:0:1組卷：134引用：1難度：0.3
解析
2．已知二次函數(shù)y=ax²+4ax+4a-1的圖象是C₁．
（1）求C₁關(guān)于點(diǎn)R（1，0）中心對(duì)稱(chēng)的圖象C₂的函數(shù)解析式；
（2）在（1）的條件下，設(shè)拋物線C₁、C₂與y軸的交點(diǎn)分別為A、B，當(dāng)AB=18時(shí)，求a的值．
發(fā)布：2025/5/28 7:0:1組卷：311引用：6難度：0.1
解析

3．先閱讀短文，再回答短文后面的問(wèn)題．
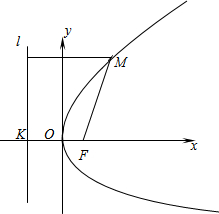
平面內(nèi)與一個(gè)定點(diǎn)F和一條定直線l的距離相等的點(diǎn)的軌跡叫做拋物線，點(diǎn)F叫做拋物線的焦點(diǎn)，直線l叫做拋物線的準(zhǔn)線．
下面根據(jù)拋物線的定義，我們來(lái)求拋物線的方程．
如圖，建立直角坐標(biāo)系xOy,使x軸經(jīng)過(guò)點(diǎn)F且垂直于直線l,垂足為K，并使原點(diǎn)與線段KF的中點(diǎn)重合．設(shè)|KF|=p（p＞0），那么焦點(diǎn)F的坐標(biāo)為（
p
2
，0），準(zhǔn)線l的方程為x=-
p
2
．
設(shè)點(diǎn)M（x,y）是拋物線上任意一點(diǎn)，點(diǎn)M到l的距離為d,由拋物線的定義，拋物線就是滿足|MF|=d的點(diǎn)M的軌跡．
∵|MF|=
（
x
-
p
2
）
2
+
y
2
，d=|x+
p
2
|∴
（
x
-
p
2
）
2
+
y
2
=|x+
p
2
|
將上式兩邊平方并化簡(jiǎn)，得y²=2px（p＞0）①
方程①叫做拋物線的標(biāo)準(zhǔn)方程，它表示的拋物線的焦點(diǎn)在x軸的正半軸上，坐標(biāo)是（
p
2
，0），它的準(zhǔn)線方程是x=-
p
2
．
一條拋物線，由于它在坐標(biāo)平面內(nèi)的位置不同，方程也不同．所以拋物線的標(biāo)準(zhǔn)方程還有其它的幾種形式：y²=-2px,x²=2py,x²=-2py.這四種拋物線的標(biāo)準(zhǔn)方程，焦點(diǎn)坐標(biāo)以及準(zhǔn)線方程列表如下：

標(biāo)準(zhǔn)方程焦點(diǎn)坐標(biāo) 準(zhǔn)線方程

y²=2px（p＞0）（
p
2
，
0
） x=-
p
2

y²=-2px（p＞0）（-
p
2
，
0
） x=
p
2

x²=2py（p＞0）（0，
p
2
） y=-
p
2

x²=-2py（p＞0）（0，-
p
2
） y=-
p
2

解答下列問(wèn)題：
（1）①已知拋物線的標(biāo)準(zhǔn)方程是y²=8x,則它的焦點(diǎn)坐標(biāo)是
，準(zhǔn)線方程是

②已知拋物線的焦點(diǎn)坐標(biāo)是F（0，-6），則它的標(biāo)準(zhǔn)方程是
．
（2）點(diǎn)M與點(diǎn)F（4，0）的距離比它到直線l：x+5=0的距離小1，求點(diǎn)M的軌跡方程．
（3）直線
y
=
3
x
+
b
經(jīng)過(guò)拋物線y²=4x的焦點(diǎn)，與拋物線相交于兩點(diǎn)A、B，求線段AB的長(zhǎng)．

發(fā)布：2025/5/28 7:0:1組卷：267引用：1難度：0.3

相關(guān)試卷