 先閱讀短文,再回答短文后面的問題.
先閱讀短文,再回答短文后面的問題.
平面內與一個定點F和一條定直線l的距離相等的點的軌跡叫做拋物線,點F叫做拋物線的焦點,直線l叫做拋物線的準線.
下面根據拋物線的定義,我們來求拋物線的方程.
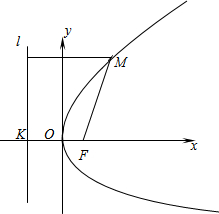
如圖,建立直角坐標系xOy,使x軸經過點F且垂直于直線l,垂足為K,并使原點與線段KF的中點重合.設|KF|=p(p>0),那么焦點F的坐標為(p2,0),準線l的方程為x=-p2.
設點M(x,y)是拋物線上任意一點,點M到l的距離為d,由拋物線的定義,拋物線就是滿足|MF|=d的點M的軌跡.
∵|MF|=(x-p2)2+y2,d=|x+p2|∴(x-p2)2+y2=|x+p2|
將上式兩邊平方并化簡,得y2=2px(p>0)①
方程①叫做拋物線的標準方程,它表示的拋物線的焦點在x軸的正半軸上,坐標是(p2,0),它的準線方程是x=-p2.
一條拋物線,由于它在坐標平面內的位置不同,方程也不同.所以拋物線的標準方程還有其它的幾種形式:y2=-2px,x2=2py,x2=-2py.這四種拋物線的標準方程,焦點坐標以及準線方程列表如下:
p
2
p
2
(
x
-
p
2
)
2
+
y
2
p
2
(
x
-
p
2
)
2
+
y
2
p
2
p
2
p
2
| 標準方程 | 焦點坐標 | 準線方程 |
| y2=2px(p>0) | ( p 2 , 0 |
x=- p 2 |
| y2=-2px(p>0) | (- p 2 , 0 |
x= p 2 |
| x2=2py(p>0) | (0, p 2 |
y=- p 2 |
| x2=-2py(p>0) | (0,- p 2 |
y=- p 2 |
(1)①已知拋物線的標準方程是y2=8x,則它的焦點坐標是
(2,0)
(2,0)
,準線方程是 x=-2
x=-2
②已知拋物線的焦點坐標是F(0,-6),則它的標準方程是
x2=-24y
x2=-24y
.(2)點M與點F(4,0)的距離比它到直線l:x+5=0的距離小1,求點M的軌跡方程.
(3)直線
y
=
3
x
+
b
【考點】二次函數綜合題.
【答案】(2,0);x=-2;x2=-24y
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/28 7:0:1組卷:268引用:1難度:0.3
相似題
-
1.OABC是一張放在平面直角坐標系中的矩形紙片,O為原點,點A在x軸上,點C在y軸上,OA=10,OC=6.
(1)如圖1,在OA上選取一點G,將△COG沿CG翻折,使點O落在BC邊上,記為E,求折痕y1所在直線的解析式;
(2)如圖2,在OC上選取一點D,將△AOD沿AD翻折,使點O落在BC邊上,記為E'.
①求折痕AD所在直線的解析式;
②再作E'F∥AB,交AD于點F.若拋物線y=-x2+h過點F,求此拋物線的解析式,并判斷它與直線AD的交點的個數.112
(3)如圖3,一般地,在OC、OA上選取適當的點D'、G',使紙片沿D'G'翻折后,點O落在BC邊上,記為E''.請你猜想:折痕D'G'所在直線與②中的拋物線會有什么關系?用(1)中的情形驗證你的猜想.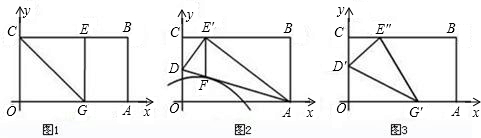 發布:2025/5/29 8:30:1組卷:184引用:8難度:0.1
發布:2025/5/29 8:30:1組卷:184引用:8難度:0.1 -
2.如圖,在Rt△ABC中,∠C=90°,AC=12,BC=16,動點P從點A出發沿AC邊向點C以每秒3個單位長的速度運動,動點Q從點C出發沿CB邊向點B以每秒4個單位長的速度運動.P,Q分別從點A,C同時
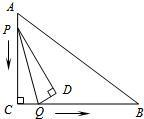 出發,當其中一點到達端點時,另一點也隨之停止運動.在運動過程中,△PCQ關于直線PQ對稱的圖形是△PDQ.設運動時間為t(秒).
出發,當其中一點到達端點時,另一點也隨之停止運動.在運動過程中,△PCQ關于直線PQ對稱的圖形是△PDQ.設運動時間為t(秒).
(1)設四邊形PCQD的面積為y,求y與t的函數關系式;
(2)t為何值時,四邊形PQBA是梯形?發布:2025/5/29 8:30:1組卷:38引用:3難度:0.1 -
3.如果二次函數y=ax2+bx+c的圖象的頂點坐標是(2,4),且直線y=x+4依次與y軸和拋物線相交于P、Q、R三點,PQ:QR=1:3,求這個二次函數解析式.
發布:2025/5/29 8:0:2組卷:148引用:1難度:0.1


