【閱讀理解】
在學(xué)習(xí)了《銳角三角函數(shù)》這一章內(nèi)容后，我們知道了30°，60°，45°這幾個(gè)特殊角的三角函數(shù)值，我們還能求出tan15°的值．
如圖1，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=1延長(zhǎng)CB到點(diǎn)D，使DB=AB，則有∠D=15°．
在Rt△ABC中，∠ABC=30°，∴AB=BD=2BC=3；
在Rt△ACD中tanD=ACDC=12+3=2-3（2+3）（2-3）=2-3；
∴tan15°=2-3．
【實(shí)際應(yīng)用】（1）2022年北京冬奧會(huì)持續(xù)點(diǎn)燃了群眾們的冰雪熱情，在“大力發(fā)展寒地冰雪經(jīng)濟(jì)”的黃金發(fā)展時(shí)期，某滑雪場(chǎng)為滿足青少年滑雪初學(xué)者的需求，設(shè)計(jì)了一條滑道AB，如圖2所示，滑道的坡角∠B=15°，水平寬度BC=100m.請(qǐng)根據(jù)以上材料提供的數(shù)據(jù)，求出圖2中滑道的鉛直高度AC是多少米？（結(jié)果取整數(shù)，參考數(shù)據(jù)3≈1.732）．
【類比探究】（2）如果滑雪場(chǎng)準(zhǔn)備再建一條坡角為22.5°的滑道，你能根據(jù)圖3求出tan22.5°的值嗎？
類比上面提供的方法，請(qǐng)你將下列探究過程補(bǔ)充完整：
解：Rt△ABC中（圖3），∠C=90°，∠B=45°，AC=1．
BC
=
3
tan
D
=
AC
DC
=
1
2
+
3
=
2
-
3
（
2
+
3
）
（
2
-
3
）
=
2
-
3
tan
15
°=
2
-
3
3
≈
1
.
732
【考點(diǎn)】解直角三角形的應(yīng)用．
【答案】（1）滑道的鉛直高度是27米．
（2）．
（2）
2
-
1
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：219引用：1難度：0.7
相似題
-
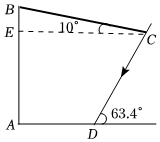1．某老年活動(dòng)中心欲在一房前3m高的前墻（AB）上安裝一遮陽篷BC，使正午時(shí)刻房前能有2m寬的陰影處（AD）以供納涼．假設(shè)此地某日正午時(shí)刻太陽光與水平地面的夾角為63.4°，遮陽篷BC與水平面的夾角為10°．如圖為側(cè)面示意圖，請(qǐng)你求出此遮陽篷BC的長(zhǎng)度（結(jié)果精確到0.1m）．
（參考數(shù)據(jù)：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18；sin63.4°≈0.89，cos63.4°≈0.45，tan63.4°≈2.00）發(fā)布：2025/5/22 16:30:1組卷：1045引用：9難度：0.5 -
2．市體育協(xié)會(huì)在天德湖公園主辦的放風(fēng)箏比賽．比賽中小軍在A處不小心讓風(fēng)箏掛在了一棵樹的樹梢上（如圖），固定在了D處，此時(shí)風(fēng)箏線AD與水平線的夾角為30°．為了便于觀察，小軍迅速向前邊移動(dòng)邊收線到達(dá)了離A處6米的B處，此時(shí)風(fēng)箏線BD與水平線的夾角為45°．已知點(diǎn)A、B、C在同一條直線上，∠ACD=90°．請(qǐng)求出此時(shí)小軍手中的風(fēng)箏線BD的長(zhǎng)度約是多少米？（本題中風(fēng)箏線均視為線段，≈1.41，2≈1.73，最后結(jié)果精確到1米）3發(fā)布：2025/5/22 17:0:1組卷：50引用：3難度：0.5 -
3．北京冬奧會(huì)開幕式的巨型雪花狀主火炬塔的設(shè)計(jì)，體現(xiàn)了環(huán)保低碳理念．如圖所示，它的主體形狀呈正六邊形．若點(diǎn)A，F(xiàn)，B，D，C，E是正六邊形的六個(gè)頂點(diǎn)，則tan∠BAC的值是 ．發(fā)布：2025/5/22 17:0:1組卷：84引用：3難度：0.6
相關(guān)試卷