問題解決：如圖1，在矩形ABCD中，點(diǎn)E，F(xiàn)分別在AB，BC邊上，DE=AF，DE⊥AF于點(diǎn)G．
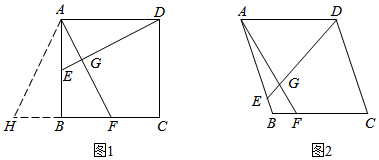
（1）求證：四邊形ABCD是正方形；
（2）延長CB到點(diǎn)H，使得BH=AE，判斷△AHF的形狀，并說明理由．
類比遷移：如圖2，在菱形ABCD中，點(diǎn)E，F(xiàn)分別在AB，BC邊上，DE與AF相交于點(diǎn)G，DE=AF，∠AED=60°，AE=5，BF=2，求DE的長．
【考點(diǎn)】四邊形綜合題．
【答案】（1）證明見解析部分；
（2）結(jié)論：△AHF是等腰三角形，證明見解析部分；
類比遷移：7．
（2）結(jié)論：△AHF是等腰三角形，證明見解析部分；
類比遷移：7．
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：266引用：4難度：0.1
相似題
-
1．已知?ABCD，BC=2．
（1）如圖1，若以BC為邊作等邊△BCE，且點(diǎn)E恰好在邊AD上，直接寫出此時(shí)?ABCD的面積；
（2）如圖2，若以BC為斜邊作等腰直角△BCF，且點(diǎn)F恰好在邊AD上，過C作CG⊥CD交BF于G，連接AG．
①依題意將圖2補(bǔ)全；
②用等式表示此時(shí)線段CD，CG，AG之間的數(shù)量關(guān)系，并證明；
（3）如圖3，以BC為邊作?BCMN，且∠CMN=60°，BN=3．若NA⊥BD，直接用等式表示此時(shí)BD與NA的數(shù)量關(guān)系．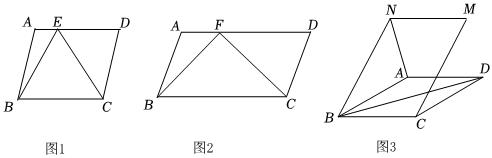
發(fā)布：2025/6/4 9:30:1組卷：338引用：1難度：0.1 -
2．如圖1，在平面直角坐標(biāo)系中，直線AB與x軸正半軸，y軸正半軸分別交于A，B兩點(diǎn)，A（6，0），∠OAB=60°，點(diǎn)P是線段AB上的任意一點(diǎn)（包括端點(diǎn)），點(diǎn)Q在直線AB上，PQ=4BP．
（1）點(diǎn)B的坐標(biāo)是 ．
（2）連結(jié)OQ，OP，若△OPQ是以PQ為底邊的等腰三角形，求△OPQ的面積．
（3）如圖2，點(diǎn)C的坐標(biāo)為，以P，Q，C，D為頂點(diǎn)作平行四邊形，若點(diǎn)D落在x軸上，求所有滿足條件的BP的長．（0，23）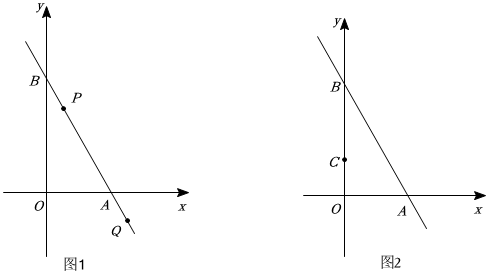
發(fā)布：2025/6/4 9:30:1組卷：30引用：1難度：0.3 -
3．如圖1，在正方形ABCD（正方形四邊相等，四個(gè)角均為直角）中，AB=8，P為線段BC上一點(diǎn)，連接AP，過B作BQ⊥AP，交CD于點(diǎn)Q，將△BQC沿BQ所在的直線對折得到△BQC′，延長QC′交AD于點(diǎn)N．
（1）求證：BP=CQ；
（2）若BP=PC，求AN的長；13
（3）如圖2，延長QN交BA的延長線于點(diǎn)M，若BP=x（0＜x＜8），△BMC′的面積為s,求s與x之間的函數(shù)關(guān)系式．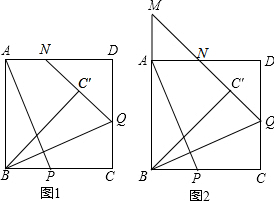
發(fā)布：2025/6/4 9:30:1組卷：147引用：1難度：0.4