問題提出
（1）如圖①，在?ABCD中，∠A=60°，AB=16，AD=12，E、H分別是AD、AB的中點，點F在DC上，且DF=10，點G在BC上，且BG=4，求四邊形FEGH的面積．（結果保留根號）
問題解決
（2）某市進行河灘治理，優化美化人居生態環境．如圖②所示，現規劃在河畔的一處灘地上規劃一個矩形河畔公園ABCD．按設計要求，要在矩形河畔公園ABCD內挖一個四邊形人工湖OPMN，使點O、P、M、N分別在邊BC、CD、AE、AB上，且滿足AN=CP，AM=OC．已知矩形ABCD中，AC為對角線，AB=800m,BC=1200m,為滿足人工湖周邊各功能場所及綠化用地需要，想讓人工湖OPMN的邊MP∥AC，且面積盡可能大．請問，是否存在符合設計要求的面積最大的四邊形人工湖OPMN？若存在，求四邊形OPMN面積的最大值及這時點N到點A的距離；若不存在，請說明理由．
【答案】（1）四邊形FEGH的面積為49；
（2）四邊形OPMN面積的最大值為480000m2，這時點N到點A的距離為400m．
3
（2）四邊形OPMN面積的最大值為480000m2，這時點N到點A的距離為400m．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：342引用：3難度：0.5
相似題
-
1．圖1是新冠疫情期間測溫員用“額溫槍”對居民張阿姨測溫時的實景圖，圖2是其側面示意圖，其中槍柄CD和手臂BC始終在同一條直線上，槍身DE與額頭F保持垂直．胳膊AB=24cm,BD=40cm,肘關節B與槍身端點E之間的水平寬度為28cm（即BH的長度），槍身DE=8cm.
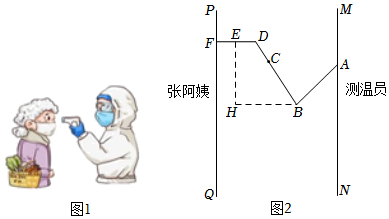
（1）求∠EDC的度數；
（2）測溫時規定槍身端點E與額頭規定范圍為3cm-5cm.在圖2中若∠ABC=75°，張阿姨與測溫員之間的距離為48cm.問此時槍身端點E與張阿姨額頭F的距離是否在規定范圍內，并說明理由．
（結果保留小數點后兩位．參考數據：2≈1.414）3≈1.732發布：2025/5/31 7:30:1組卷：2299引用：13難度：0.5 -
2．閱讀下列材料：
在△ABC中，∠A、∠B、∠C所對的邊分別為a、b、c,求證：=asinA．bsinB
證明：如圖1，過點C作CD⊥AB于點D，則：
在Rt△BCD中，CD=asinB
在Rt△ACD中，CD=bsinA
∴asinB=bsinA
∴=asinAbsinB
根據上面的材料解決下列問題：
（1）如圖2，在△ABC中，∠A、∠B、∠C所對的邊分別為a、b、c,求證：=bsinB；csinC
（2）為了辦好湖南省首屆旅游發展大會，張家界市積極優化旅游環境．如圖3，規劃中的一片三角形區域需美化，已知∠A=67°，∠B=53°，AC=80米，求這片區域的面積．（結果保留根號．參考數據：sin53°≈0.8，sin67°≈0.9）
發布：2025/5/30 23:0:1組卷：1418引用：7難度：0.6 -
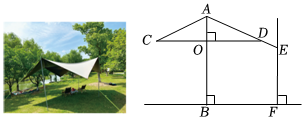3．夏秋季節，許多露營愛好者晚間會在湖邊露營，為遮陽和防雨會搭建一種“天幕”，其截面示意圖是軸對稱圖形，對稱軸是垂直于地面的支桿AB，用繩子拉直AD后系在樹干EF上的點E處（EF⊥BF），使得A，D，E在一條直線上，通過調節點E的高度可控制“天幕”的開合，幕布寬AC=AD=2m,CD⊥AB于點O，支桿AB與樹干EF的橫向距離BF=2.2m.（參考數據：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）
（1）天晴時打開“天幕”，若∠CAE=140°，求遮陽寬度CD．
（2）下雨時收攏“天幕”，∠CAE由140°減小到90°，求點E下降的高度．發布：2025/5/31 15:30:1組卷：368引用：3難度：0.6