問題的提出：如果點P是銳角△ABC內(nèi)一動點，如何確定一個位置，使點P到△ABC的三頂點的距離之和PA+PB+PC的值為最小？
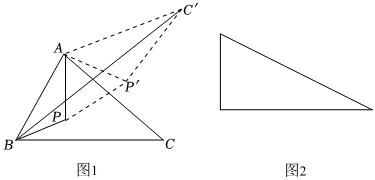
（1）問題的轉(zhuǎn)化：把△APC繞點A逆時針旋轉(zhuǎn)60°得到△AP′C′，連接PP′，這樣就把確定PA+PB+PC的最小值的問題轉(zhuǎn)化成確定BP+PP′+P′C的最小值的問題了，請你利用圖1證明：PA+PB+PC=BP+PP′+P′C′；
（2）問題的解決：當(dāng)點P到銳角△ABC的三頂點的距離之和PA+PB+PC的值為最小時，求∠APB和∠APC的度數(shù)；
（3）問題的延伸：如圖2是有一個銳角為30°的直角三角形，如果斜邊為2，點P是這個三角形內(nèi)一動點，請你利用以上方法，求點P到這個三角形各頂點的距離之和的最小值．
【考點】幾何變換綜合題．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/17 8:0:9組卷：964引用：3難度：0.1
相似題
-
1．綜合與實踐：
在綜合與實踐課上，老師讓同學(xué)們以“矩形紙片的折疊”為主題開展數(shù)學(xué)活動．
在矩形ABCD中，E為AB邊上一點，F(xiàn)為AD邊上一點，連接CE、CF，分別將△BCE和△CDF沿CE、CF翻折，點D、B的對應(yīng)點分別為點G、H，且C、H、G三點共線．
（1）如圖1，若F為AD邊的中點，AB=BC=6，點G與點H重合，則∠ECF=°，BE=；
（2）如圖2，若F為AD的中點，CG平分∠ECF，，BC=2，求∠ECF的度數(shù)及BE的長．AB=2+1
（3）AB=5，AD=3，若F為AD的三等分點，請直接寫出BE的長．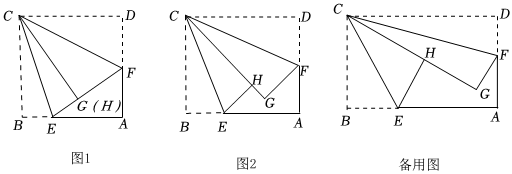
發(fā)布：2025/5/22 5:30:2組卷：902引用：5難度：0.4 -
2．問題背景：如圖1，在等腰△ABC中，AB=AC，AD⊥BC，垂足為點D，在△AEF中，∠AEF=90°，
，連接BF，M是BF中點，連接EM和DM，在△AEF繞點A旋轉(zhuǎn)過程中，線段EM和DM之間存在怎樣的數(shù)量關(guān)系？∠EAF=12∠BAC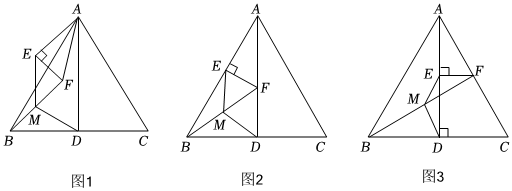
觀察發(fā)現(xiàn)：
（1）為了探究線段EM和DM之間的數(shù)量關(guān)系，可先將圖形位置特殊化，將△AEF繞點A旋轉(zhuǎn)，使AE與AB重合，如圖2，易知EM和DM之間的數(shù)量關(guān)系為 ；
操作證明：
（2）繼續(xù)將△AEF繞點A旋轉(zhuǎn)，使AE與AD重合時，如圖3，（1）中線段EM和DM之間的數(shù)量關(guān)系仍然成立，請加以證明．
問題解決：
（3）根據(jù)上述探究的經(jīng)驗，我們回到一般情況，如圖1，在其他條件不變的情況下，上述的結(jié)論還成立嗎？請說明你的理由．發(fā)布：2025/5/22 6:30:1組卷：219引用：2難度：0.1 -
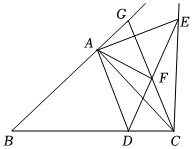3．如圖，在△ABC中，AB=AC，∠BAC=90°，D為線段BC上一點，連接AD，將線段AD繞點A逆時針旋轉(zhuǎn)90°得到線段AE，作射線CE．
（1）求證：△BAD≌△CAE，并求∠BCE的度數(shù)；
（2）若F為DE中點，連接AF，連接CF并延長，交射線BA于點G．當(dāng)BD=2，DC=1時，
①求AF的長；
②直接寫出CG的長．發(fā)布：2025/5/22 4:30:1組卷：516引用：4難度：0.5